题目内容
(本小题满分12分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值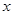 (单位:元,
(单位:元,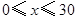 )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成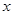 的函数;(II)如何定价才能使一个星期的商品销售利润最大?
的函数;(II)如何定价才能使一个星期的商品销售利润最大?
(I)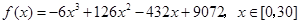 (II)
(II)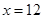 时利润最大.
时利润最大.
解析试题分析:(Ⅰ)设商品降价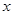 元,则多卖的商品数为
元,则多卖的商品数为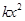 ,若记商品在一个星期的获利为
,若记商品在一个星期的获利为 ,
,
则依题意有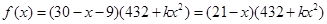 ,
,
又由已知条件, ,于是有
,于是有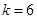 ,所以
,所以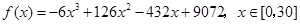 .
.
(Ⅱ)根据(Ⅰ),我们有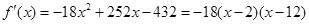 .
.
故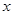
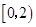
2 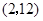
12 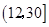
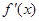
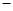
0 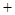
0 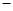


极小 
极大 
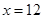 时,
时, 达到极大值.因为
达到极大值.因为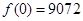 ,
,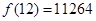 ,所以定价为
,所以定价为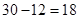 元能使一个星期的商品销售利润最大.
元能使一个星期的商品销售利润最大.
考点:函数模型的选择与应用.
点评:本小题主要考查根据实际问题建立数学模型,以及运用函数、导数的知识解决实际问题的能力.利用导数求函数的最值是解决本题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
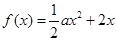 ,
,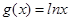 .
.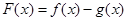 ,求函数
,求函数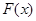 的单调区间;
的单调区间; 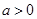 ,使得方程
,使得方程 在区间
在区间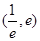 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.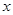 元/千克,政府补贴为
元/千克,政府补贴为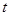 元/千克,根据市场调查,当
元/千克,根据市场调查,当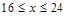 时,这种食品市场日供应量
时,这种食品市场日供应量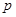 万千克与市场日需量
万千克与市场日需量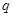 万千克近似地满足关系:
万千克近似地满足关系: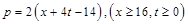 ,
,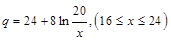 。当
。当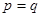 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。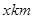 ,建在C处的垃圾处理厂对城A和城B的总影响度为
,建在C处的垃圾处理厂对城A和城B的总影响度为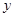 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。

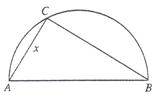
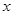 的函数;
的函数; (2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。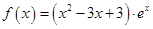 ,设
,设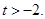
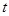 的取值范围,使得函数
的取值范围,使得函数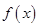 在
在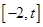 上为单调函数;
上为单调函数; 满足
满足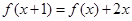 且
且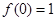 .
.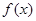 的解析式;
的解析式; 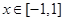 时,不等式:
时,不等式: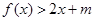 恒成立,求实数
恒成立,求实数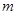 的范围.
的范围.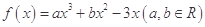 在点
在点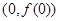 处的切线与直线
处的切线与直线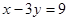 垂直.
垂直.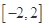 上任意两个自变量的值
上任意两个自变量的值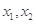 都有
都有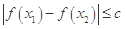 ,求实数
,求实数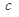 的最小值;
的最小值;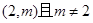 可作曲线
可作曲线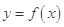 的三条切线,求实数
的三条切线,求实数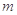 的取值范围.
的取值范围.