题目内容
已知函数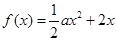 ,
,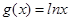 .
.
(1)设函数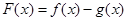 ,求函数
,求函数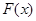 的单调区间;
的单调区间;
(2)是否存在实数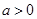 ,使得方程
,使得方程 在区间
在区间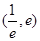 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(Ⅱ) (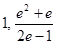 ) .
) .
解析试题分析:(I)因为,函数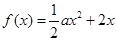 ,
,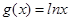 .
.
所以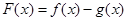 =
=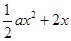 -lnx,其定义域为(0,+
-lnx,其定义域为(0,+ )。
)。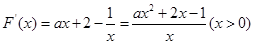 ,
,
当a=0时,由f′(x)>0,得,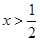 ,故f(x)在(
,故f(x)在(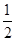 ,+∞)上单调递增,在(0,
,+∞)上单调递增,在(0,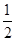 )单调递减;
)单调递减;
当a>0时,由f′(x)>0,得,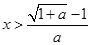 ,故f(x)在(
,故f(x)在(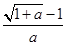 ,+∞)上单调递增,在(0,
,+∞)上单调递增,在(0,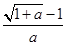 )单调递减;
)单调递减;
当a<0时,由f′(x)>0,得,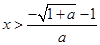 ,故f(x)在(
,故f(x)在(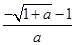 ,+∞)上单调递增,在(0,
,+∞)上单调递增,在(0,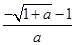 )单调递减。
)单调递减。
(Ⅱ)把方程 整理为
整理为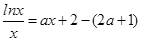 ,
,
即为方程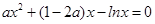 . 5分
. 5分
设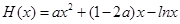
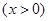 ,原方程在区间(
,原方程在区间(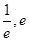 )内有且只有两个不相等的实数根, 即为函数
)内有且只有两个不相等的实数根, 即为函数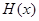 在区间(
在区间(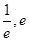 )内有且只有两个零点. 6分
)内有且只有两个零点. 6分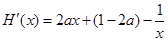
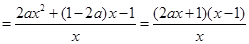 7分
7分
令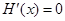 ,因为
,因为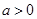 ,解得
,解得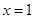 或
或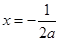 (舍) 8分
(舍) 8分
当 时,
时, 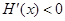 ,
, 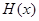 是减函数;当
是减函数;当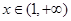 时,
时, 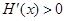 ,
,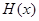 是增函数 10分
是增函数 10分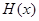 在(
在(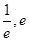 )内有且只有两个不相等的零点, 只需
)内有且只有两个不相等的零点, 只需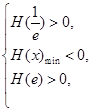
即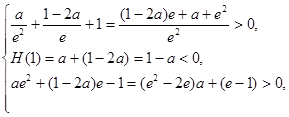 ∴
∴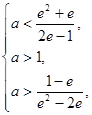
解得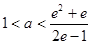 , 所以
, 所以 的取值范围是(
的取值范围是(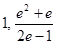 ) .
) .
考点:本题主要考查应用导数研究函数的单调性、最值及不等式恒成立问题,函数零点,不等式的解法。
点评:难题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。(I)中要对a的不同取值情况加以讨论,在解不等式取舍过程中易于出错。涉及不等式恒成立问题,转化成了研究函数的最值,通过构建a的不等式组,求得a的范围。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
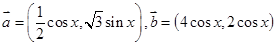 函数
函数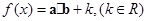
 的单调增区间;
的单调增区间;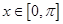 时,
时,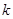 的值.
的值. 在
在 上是增函数,q:函数
上是增函数,q:函数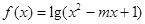 的定义域为R.
的定义域为R.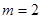 ,试判断命题p的真假;
,试判断命题p的真假; 的取值范围.
的取值范围.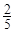 小时,种植一捆沙棘树苗用时
小时,种植一捆沙棘树苗用时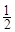 小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
小时.应如何分配A,B两组的人数,使植树活动持续时间最短?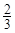 小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.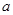 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。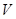 表示为
表示为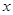 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,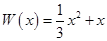 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,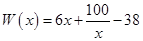 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.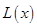 (万元)关于年产量
(万元)关于年产量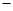 固定成本
固定成本 的值.(参考数据:ln2»0.69,ln10»2.3)
的值.(参考数据:ln2»0.69,ln10»2.3)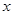 (单位:元,
(单位:元,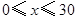 )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成