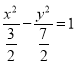Question

【题目】已知函数f（x）=ax3﹣x2+4x+3，若在区间[﹣2，1]上，f（x）≥0恒成立，则a的取值范围是（ ）
A.[﹣6，﹣2]
B.
C.[﹣5，﹣3]
D.[﹣4，﹣3]

Answer 1

【答案】A
【解析】解：解：当x=0时，不等式ax3﹣x2+4x+3≥0对任意a∈R恒成立； 当0＜x≤1时，ax3﹣x2+4x+3≥0可化为a≥ ，
令f（x）= ﹣ ，则f′（x）=﹣ + =﹣ （*），
当0＜x≤1时，f′（x）＞0，f（x）在（0，1]上单调递增，
f（x）max=f（1）=﹣6，∴a≥﹣6；
当﹣2≤x＜0时，ax3﹣x2+4x+3≥0可化为a≤ ﹣ ，
由（*）式可知，当﹣2≤x＜﹣1时，f′（x）＜0，f（x）单调递减，
当﹣1＜x＜0时，f′（x）＞0，f（x）单调递增，
f（x）min=f（﹣1）=﹣2，∴a≤﹣2；
综上所述，实数a的取值范围是﹣6≤a≤﹣2，即实数a的取值范围是[﹣6，﹣2]．
所以答案是：[﹣6，﹣2]．
【考点精析】根据题目的已知条件，利用函数单调性的判断方法和函数的最值及其几何意义的相关知识可以得到问题的答案，需要掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较；利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值．