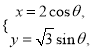题目内容
【题目】=2sin(ωx+φ),x∈R,其中ω>0,﹣π<φ≤π.若函数f(x)的最小正周期为6π,且当x=![]() 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )
A. f(x)在区间[﹣2π,0]上是增函数B. f(x)在区间[﹣3π,﹣π]上是增函数
C. f(x)在区间[3π,5π]上是减函数D. f(x)在区间[4π,6π]上是减函数
【答案】A
【解析】
试题由函数f(x)的最小正周期为6π,根据周期公式可得ω=![]() ,且当x=
,且当x=![]() 时,f(x)取得最大值,代入可得,2sin(
时,f(x)取得最大值,代入可得,2sin(![]() φ)=2,结合已知﹣π<φ≤π可得φ=
φ)=2,结合已知﹣π<φ≤π可得φ=![]() 可得
可得![]() ,分别求出函数的单调增区间和减区间,结合选项验证即可
,分别求出函数的单调增区间和减区间,结合选项验证即可
解:∵函数f(x)的最小正周期为6π,根据周期公式可得ω=![]() ,
,
∴f(x)=2sin(![]() φ),
φ),
∵当x=![]() 时,f(x)取得最大值,∴2sin(
时,f(x)取得最大值,∴2sin(![]() φ)=2,
φ)=2,
∵﹣π<φ≤π,∴φ=![]() ,∴
,∴![]() ,
,
由![]() 可得函数的单调增区间:
可得函数的单调增区间:![]() ,
,
由![]() 可得函数的单调减区间:
可得函数的单调减区间:![]() ,
,
结合选项可知A正确,
故选A.

 名校课堂系列答案
名校课堂系列答案【题目】207年8月8日晚我国四川九赛沟县发生了7.0级地震,为了解与掌握一些基本的地震安全防护知识,某小学在9月份开学初对全校学生进行了为期一周的知识讲座,事后并进行了测试(满分100分),根据测试成绩评定为“合格”(60分以上包含60分)、“不合格”两个等级,同时对相应等级进行量化:“合格”定为10分,“不合格”定为5分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
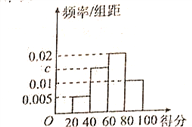
(1)求![]() 的值;
的值;
(2)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈,现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)设函数![]() (其中
(其中![]() 表示
表示![]() 的方差)是评估安全教育方案成效的一种模拟函数.当
的方差)是评估安全教育方案成效的一种模拟函数.当![]() 时,认定教育方案是有效的;否则认定教育方案应需调整,试以此函数为参考依据.在(2)的条件下,判断该校是否应调整安全教育方案?
时,认定教育方案是有效的;否则认定教育方案应需调整,试以此函数为参考依据.在(2)的条件下,判断该校是否应调整安全教育方案?
【题目】某地植被面积 ![]() (公顷)与当地气温下降的度数
(公顷)与当地气温下降的度数![]() (
(![]() )之间有如下的对应数据:
)之间有如下的对应数据:
| 20 | 40 | 50 | 60 | 80 |
| 3 | 4 | 4 | 4 | 5 |
(1)请用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少![]() ?
?
参考公式:用最小二乘法求线性回归方程系数公式: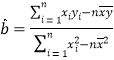 ,
,![]() .
.
【题目】2017年11月、12月全国大范围流感爆发,为研究昼夜温差大小与患感冒人数多少之间的关系,一兴趣小组抄录了某医院11月到12月间的连续6个星期的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 | 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | 第六周 |
昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验。
(Ⅰ)求选取的2组数据恰好是相邻两个星期的概率;
(Ⅱ)若选取的是第一周与第六周的两组数据,请根据第二周到第五周的4组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式: 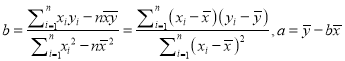 )
)
参考数据: ![]() 1092,
1092, ![]() 498
498