题目内容
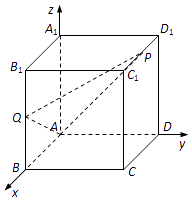
【题目】如图，在平面直角坐标系xOy中，已知椭圆 
（a＞b＞0）的离心率为 
，焦点到相应准线的距离为1．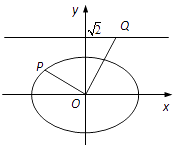 
（1）求椭圆的标准方程；
（2）若P为椭圆上的一点，过点O作OP的垂线交直线 
于点Q，求 
的值．
【答案】
（1）解：由题意得， 
， 
，
解得 
，c=1，b=1．
所以椭圆的方程为 
（2）解：由题意知OP的斜率存在．
当OP的斜率为0时， 
， 
，所以 
．
当OP的斜率不为0时，设直线OP方程为y=kx．
由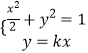 
得（2k2+1）x2=2，解得 
，所以 
，
所以 
．
因为OP⊥OQ，所以直线OQ的方程为 
．
由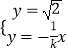 
得 
，所以OQ2=2k2+2．
所以 
．
综上，可知
【解析】（1）由已知条件可得 ， ，然后求解椭圆的方程．（2）由题意知OP的斜率存在．当OP的斜率为0时，求解结果；当OP的斜率不为0时，设直线OP方程为y=kx．联立方程组，推出 ．OQ2=2k2+2．然后求解即可．
【考点精析】通过灵活运用椭圆的标准方程，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
即可以解答此题．
黄冈天天练口算题卡系列答案
【题目】某险种的基本保费为
（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下：
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
（1）求一续保人本年度的保费高于基本保费的概率；
（2）已知一续保人本年度的保费高于基本保费，求其保费比基本保费高出
的概率.
【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示，其中成绩分组区间是
，
，
，
，
.
（1）求图中
的值；
（2）根据频率分布直方图，估计这200名学生的平均分；
（3）若这200名学生的数学成绩中，某些分数段的人数
与英语成绩相应分数段的人数
之比如下表所示，求英语成绩在
的人数.
分数段 |
|
|
|
|
|
| 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
【题目】为了参加某运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
队别 | 北京 | 上海 | 天津 | 八一 |
人数 | 4 | 6 | 3 | 5 |
(1)从这18名队员中随机选出两名,求两人来自同一队的概率;
(2)若要求选出两名队员担任正副队长,设其中来自北京队的人数为
,求随机变量的分布列.
