题目内容
已知函数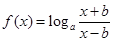
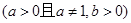 .
.
(1)求 的定义域;
的定义域;
(2)讨论 的奇偶性;
的奇偶性;
(3)讨论 在
在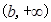 上的单调性.
上的单调性.
(1) 的定义域
的定义域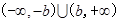 ; (2)
; (2) 为奇函数;
为奇函数;
(3)当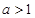 时,
时, 在
在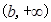 上是减函数,当
上是减函数,当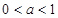 时,
时, 在
在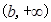 上是增函数.
上是增函数.
解析试题分析:(1)真数要大于0;
(2)用奇偶性定义讨论;
(3)先转化函数再用单调性定义讨论.
解:(1)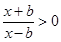 ,即
,即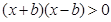 ,而
,而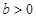 ,
,
得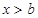 ,或
,或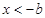 ,
,
即 的定义域
的定义域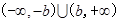 ; ---------------4分
; ---------------4分
(2)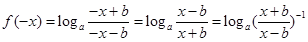 ,
,
即 ,
,
得 为奇函数; ---------------8分
为奇函数; ---------------8分
(3)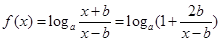 ,
,
令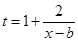 ,在
,在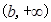 上,
上,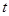 是减函数, ----------------------------10分
是减函数, ----------------------------10分
当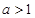 时,
时, 在
在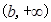 上是减函数, ----------------------------12分
上是减函数, ----------------------------12分
当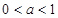 时,
时, 在
在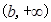 上是增函数. -------------------14分
上是增函数. -------------------14分
考点:本题主要考查了函数的基本性质单调性和奇偶性,是函数中的常考题型,属中高档题.
点评:解决该试题的关键是首先是对于定义域的准确求解,然后结合奇偶函数的定义得到奇偶性的判定,以及函数单调性的确定。

练习册系列答案
相关题目
 对任意的实数
对任意的实数 ,
, ,均有
,均有 ,则称函数
,则称函数 上的“平缓函数”.
上的“平缓函数”.  和
和 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由; 对所有的正整数
对所有的正整数 都有
都有  ,设
,设 ,
,  .
. (
( ,
,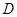 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数
 ,使函数
,使函数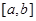 上的值域为
上的值域为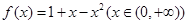 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;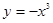 (
(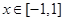 )为闭函数;
)为闭函数; 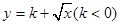 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.  定义在R上的偶函数,当
定义在R上的偶函数,当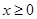 时,
时,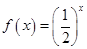
 .
. 时,求函数
时,求函数 在
在 上的最大值;
上的最大值; ,若函数
,若函数 有零点,求
有零点,求 的取值范围.
的取值范围.  ,
,  ,求:
,求: 的定义域。 (2)求使
的定义域。 (2)求使 的
的 的取值范围。
的取值范围。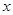 )=
)=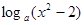 , 若
, 若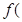 2)=1;
2)=1;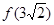 的值;
的值;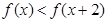
 的函数
的函数 同时满足:
同时满足: ,总有
,总有 ; ②
; ② ;
; ,则有
,则有 成立。
成立。 的值;
的值; ,总有
,总有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。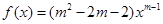 为偶函数,且在区间
为偶函数,且在区间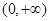 上是单调递减函数,
上是单调递减函数, 的解析式;
的解析式;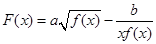 的奇偶性。 (12分)
的奇偶性。 (12分)