题目内容
设函数 .
.
(1)当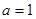 ,
,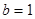 时,求所有使
时,求所有使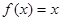 成立的
成立的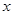 的值。
的值。
(2)若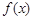 为奇函数,求证:
为奇函数,求证: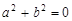 ;
;
(3)设常数 <
<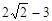 ,且对任意x
,且对任意x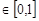 ,
,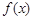 <0恒成立,求实数
<0恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)当
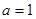 ,
,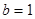 时,求所有使
时,求所有使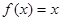 成立的
成立的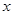 的值。
的值。(2)若
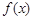 为奇函数,求证:
为奇函数,求证: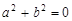 ;
;(3)设常数
 <
<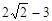 ,且对任意x
,且对任意x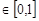 ,
,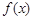 <0恒成立,求实数
<0恒成立,求实数 的取值范围.
的取值范围.解:(1)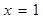 或
或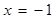 ;(2)见解析 ;(3)
;(2)见解析 ;(3)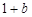 <
<  <
<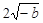 .
.
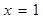 或
或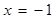 ;(2)见解析 ;(3)
;(2)见解析 ;(3)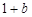 <
<  <
<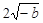 .
. 本试题主要是考查了函数的奇偶性与函数与不等式关系的运用,以及函数解析式的综合运用。
(1)当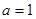 ,
,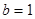 时,函数
时,函数 .
.
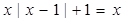
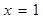 或
或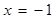
(2)若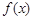 为奇函数,则对任意的
为奇函数,则对任意的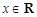 都有
都有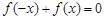 恒成立,则展开可得。
恒成立,则展开可得。
(3)由 <
<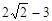 <0, 当x=0时
<0, 当x=0时 取任意实数不等式恒成立.
取任意实数不等式恒成立.
当0<x≤1时,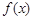 <0恒成立,也即
<0恒成立,也即 <
< <
<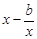 恒成立.
恒成立.
从而构造函数得到结论。
解:(1)当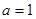 ,
,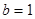 时,函数
时,函数 .
.
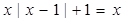
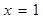 或
或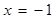
(2) 若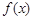 为奇函数,则对任意的
为奇函数,则对任意的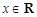 都有
都有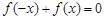 恒成立,
恒成立,
即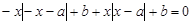 ,
,
令x=0得b=0,令x=a得a=0,∴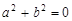
(3)由 <
<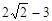 <0, 当x=0时
<0, 当x=0时 取任意实数不等式恒成立.
取任意实数不等式恒成立.
当0<x≤1时,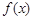 <0恒成立,也即
<0恒成立,也即 <
< <
<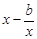 恒成立.
恒成立.
令 在0<x≤1上单调递增,∴
在0<x≤1上单调递增,∴ >
> .
.
令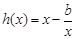 ,则
,则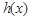 在
在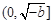 上单调递减,
上单调递减,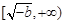 单调递增
单调递增
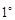 当
当 <
<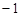 时,
时,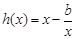 在0<x≤1上单调递减;
在0<x≤1上单调递减;
∴ <
<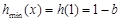 ,∴
,∴ 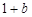 <
< <
< .
.
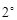 当
当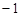 ≤
≤ <
<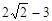 时
时 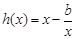 ≥
≥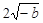 .
.
∴ <
<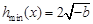 .∴
.∴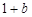 <
<  <
<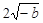 .
.
(1)当
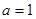 ,
,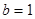 时,函数
时,函数 .
.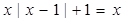
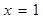 或
或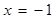
(2)若
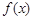 为奇函数,则对任意的
为奇函数,则对任意的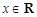 都有
都有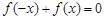 恒成立,则展开可得。
恒成立,则展开可得。(3)由
 <
<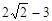 <0, 当x=0时
<0, 当x=0时 取任意实数不等式恒成立.
取任意实数不等式恒成立.当0<x≤1时,
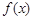 <0恒成立,也即
<0恒成立,也即 <
< <
<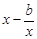 恒成立.
恒成立.从而构造函数得到结论。
解:(1)当
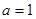 ,
,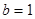 时,函数
时,函数 .
.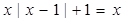
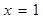 或
或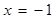
(2) 若
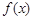 为奇函数,则对任意的
为奇函数,则对任意的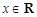 都有
都有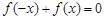 恒成立,
恒成立,即
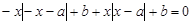 ,
,令x=0得b=0,令x=a得a=0,∴
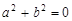
(3)由
 <
<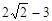 <0, 当x=0时
<0, 当x=0时 取任意实数不等式恒成立.
取任意实数不等式恒成立.当0<x≤1时,
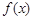 <0恒成立,也即
<0恒成立,也即 <
< <
<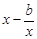 恒成立.
恒成立.令
 在0<x≤1上单调递增,∴
在0<x≤1上单调递增,∴ >
> .
. 令
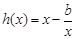 ,则
,则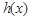 在
在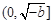 上单调递减,
上单调递减,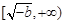 单调递增
单调递增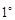 当
当 <
<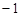 时,
时,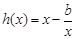 在0<x≤1上单调递减;
在0<x≤1上单调递减;∴
 <
<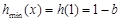 ,∴
,∴ 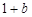 <
< <
< .
. 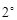 当
当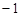 ≤
≤ <
<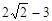 时
时 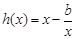 ≥
≥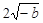 .
.∴
 <
<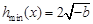 .∴
.∴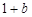 <
<  <
<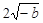 .
.
练习册系列答案
相关题目
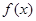 是定义在
是定义在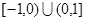 上的偶函数,当
上的偶函数,当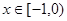 时,
时,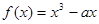 (
(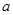 是实数)。
是实数)。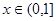 时,求f(x)的解析式;
时,求f(x)的解析式;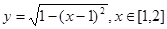 对于满足
对于满足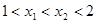 的任意
的任意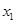 ,
,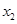 ,给出下列结论:
,给出下列结论: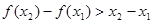 ; ②
; ②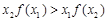 ;
;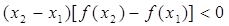 . ④
. ④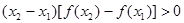
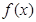 满足
满足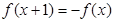 ,且在[-1,0]上单调递增,
,且在[-1,0]上单调递增,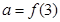 ,
,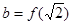 ,
,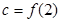 ,则
,则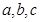 从大到小的排列顺序是 .
从大到小的排列顺序是 .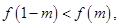 求实数m的取值范围.
求实数m的取值范围.
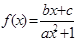 (
(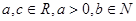 )是奇函数,
)是奇函数,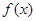 有最大值
有最大值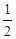
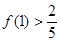 .
.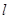 与
与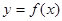 的图象交于P、Q两点,并且使得
的图象交于P、Q两点,并且使得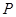 、
、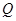 两点关于点
两点关于点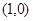 对称,若存在,求出直线
对称,若存在,求出直线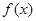 是定义在(0,+∞)上的单调增函数,满足:
是定义在(0,+∞)上的单调增函数,满足: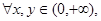 恒有
恒有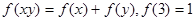 ,求:
,求: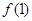 ;
;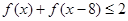 ,求
,求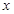 的取值范围。
的取值范围。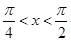 ,则函数
,则函数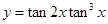 的最大值为 .
的最大值为 .