题目内容
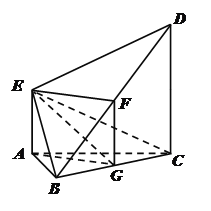
【题目】如图,△![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求![]() 点到平面
点到平面![]() 的距离.
的距离.
【答案】(1)证明见解析.
(2)![]()
【解析】分析:(1)先取![]() 边的中点
边的中点![]() ,
,![]() 的中点为
的中点为![]() ,根据三角形中位线性质得四边形
,根据三角形中位线性质得四边形![]() 为平行四边形,即得
为平行四边形,即得![]() ∥
∥![]() .再根据正三角形性质得
.再根据正三角形性质得![]()
![]() ,即得
,即得![]()
![]() .又根据
.又根据![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,易得
,易得![]()
![]() , 即得
, 即得![]()
![]() .由线面垂直判定定理得
.由线面垂直判定定理得![]() 平面
平面![]() ,最后根据面面垂直判定定理得结论,(2)先求三棱锥
,最后根据面面垂直判定定理得结论,(2)先求三棱锥![]() 体积,再根据等体积法求
体积,再根据等体积法求![]() 点到平面
点到平面![]() 的距离.
的距离.
详解:(1)取![]() 边的中点
边的中点![]() ,
,![]() 的中点为
的中点为![]() ,
,
连接![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() .
.
因为![]() 是△
是△![]() 的中位线,由题设
的中位线,由题设
![]() ∥
∥![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 为平行四边形,于是
为平行四边形,于是![]() ∥
∥![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
![]() ,
,
所以![]()
![]() ,故
,故![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() ,又
,又![]() 面
面![]() ,
,
故平面![]() 平面
平面![]() .
.
(2)由(1)![]() ,△
,△![]() 面积为2,所以三棱锥
面积为2,所以三棱锥![]() 的体积为
的体积为![]() .
.
由(1)![]() ,
,![]() ,△
,△![]() 面积为2.
面积为2.
设![]() 点到平面
点到平面![]() 的距离为
的距离为![]() ,则三棱锥
,则三棱锥![]() 的体积为
的体积为![]() .
.
因为三棱锥![]() 与三棱锥
与三棱锥![]() 的体积相等,所以
的体积相等,所以![]() ,即
,即![]() 点到平面
点到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
相关题目
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况.在30名男性驾驶员中,平均车速超过100![]() 额有20人,不超过100
额有20人,不超过100 ![]() 的有10人;在20名女性驾驶员中,平均车速超过100
的有10人;在20名女性驾驶员中,平均车速超过100![]() 的有5人,不超过100
的有5人,不超过100![]() 的有15人.
的有15人.
(1)完成下面的列联表:
平均车速超过100 | 平均车速不超过100 | 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
(2)判断是否有99.5%的把握认为,平均车速超过100![]() 与性别有关.
与性别有关.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()

