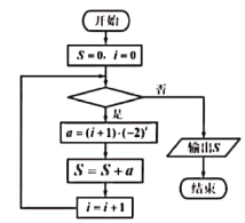
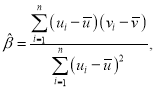题目内容
【题目】已知函数![]() .
.
(1)若函数![]() ,求
,求![]() 的极值;
的极值;
(2)证明:![]() .
.
(参考数据:![]()
![]()
![]()
![]() )
)
【答案】(1)见解析;(2)见证明
【解析】
(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(2)问题转化为证ex﹣x2﹣xlnx﹣1>0,根据xlnx≤x(x﹣1),问题转化为只需证明当x>0时,ex﹣2x2+x﹣1>0恒成立,令k(x)=ex﹣2x2+x﹣1,(x≥0),根据函数的单调性证明即可.
(1)![]() ,
,![]() ,当
,当![]() ,
,![]() ,
,
当![]() ,
,![]() ,
,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,![]() 在
在![]() 取得极大值,极大值为
取得极大值,极大值为![]() ,无极大值.
,无极大值.
(2)要证f(x)+1<ex﹣x2.
即证ex﹣x2﹣xlnx﹣1>0,
先证明lnx≤x﹣1,取h(x)=lnx﹣x+1,则h′(x)=![]() ,
,
易知h(x)在(0,1)递增,在(1,+∞)递减,
故h(x)≤h(1)=0,即lnx≤x﹣1,当且仅当x=1时取“=”,
故xlnx≤x(x﹣1),ex﹣x2﹣xlnx≥ex﹣2x2+x﹣1,
故只需证明当x>0时,ex﹣2x2+x﹣1>0恒成立,
令k(x)=ex﹣2x2+x﹣1,(x≥0),则k′(x)=ex﹣4x+1,
令F(x)=k′(x),则F′(x)=ex﹣4,令F′(x)=0,解得:x=2ln2,
∵F′(x)递增,故x∈(0,2ln2]时,F′(x)≤0,F(x)递减,即k′(x)递减,
x∈(2ln2,+∞)时,F′(x)>0,F(x)递增,即k′(x)递增,
且k′(2ln2)=5﹣8ln2<0,k′(0)=2>0,k′(2)=e2﹣8+1>0,
由零点存在定理,可知x1∈(0,2ln2),x2∈(2ln2,2),使得k′(x1)=k′(x2)=0,
故0<x<x1或x>x2时,k′(x)>0,k(x)递增,当x1<x<x2时,k′(x)<0,k(x)递减,故k(x)的最小值是k(0)=0或k(x2),由k′(x2)=0,得![]() =4x2﹣1,
=4x2﹣1,
k(x2)=![]() ﹣2
﹣2![]() +x2﹣1=﹣(x2﹣2)(2x2﹣1),∵x2∈(2ln2,2),∴k(x2)>0,
+x2﹣1=﹣(x2﹣2)(2x2﹣1),∵x2∈(2ln2,2),∴k(x2)>0,
故x>0时,k(x)>0,原不等式成立.

 名校课堂系列答案
名校课堂系列答案【题目】我国在2018年社保又出新的好消息,之前流动就业人员跨地区就业后,社保转移接续的手续往往比较繁琐,费时费力.社保改革后将简化手续,深得流动就业人员的赞誉.某市社保局从2018年办理社保的人员中抽取300人,得到其办理手续所需时间(天)与人数的频数分布表:
时间 |
|
|
|
|
|
|
人数 | 15 | 60 | 90 | 75 | 45 | 15 |
(1)若300名办理社保的人员中流动人员210人,非流动人员90人,若办理时间超过4天的人员里非流动人员有60人,请完成办理社保手续所需时间与是否流动人员的列联表,并判断是否有95%的把握认为“办理社保手续所需时间与是否流动人员”有关.
列联表如下
流动人员 | 非流动人员 | 总计 | |
办理社保手续所需 时间不超过4天 | |||
办理社保手续所需 时间超过4天 | 60 | ||
总计 | 210 | 90 | 300 |
(2)为了改进工作作风,提高效率,从抽取的300人中办理时间为![]() 流动人员中利用分层抽样,抽取12名流动人员召开座谈会,其中3人要求交书面材料,3人中办理的时间为
流动人员中利用分层抽样,抽取12名流动人员召开座谈会,其中3人要求交书面材料,3人中办理的时间为![]() 的人数为
的人数为![]() ,求出
,求出![]() 分布列及期望值.
分布列及期望值.
附: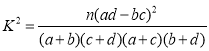
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |