题目内容
设数列{an}是一个公差为 的等差数列,已知它的前10项和为
的等差数列,已知它的前10项和为 ,且a1,a2,a4 成等比数列.
,且a1,a2,a4 成等比数列.
(1)求数列{an}的通项公式;
(2)若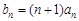 ,求数列
,求数列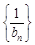 的前
的前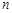 项和Tn .
项和Tn .
(1) (2)Tn
(2)Tn
解析试题分析:(1)由等差数列的求和公式代入已知条件可得d的值,进而可得a1的值,可得通项公式;(2)可得
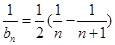 ,裂项相消法可得其和.
,裂项相消法可得其和.
试题解析:(1)设数列{an}的前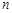 项和为
项和为 ,
,
∵S10 = 110,∴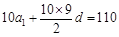 .
.
则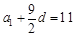 .①
.①
∵a1,a2,a4 成等比数列,
∴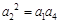 ,即
,即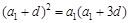 .∴
.∴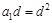 .
.
∵d ¹ 0,∴a1 = d.②
由①,②解得 ,∴
,∴ .
.
(2)∵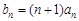 =
=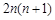 ,
,
∴ .
.
∴
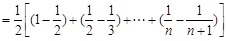
 .
.
考点:等差数列的通项公式和求和公式,裂项相消法求数列的和.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,公比
,公比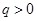 ,已知
,已知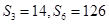 .
.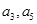 分别为等差数列
分别为等差数列 的第4项和第16项,试求数列
的第4项和第16项,试求数列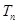 .
.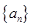 满足
满足 ,
,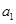 ,
,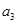 ,
,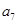 成等比数列.
成等比数列. 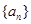 的通项公式;(2)数列
的通项公式;(2)数列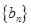 满足
满足 ,求数列
,求数列 项和
项和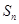 ;(Ⅲ)设
;(Ⅲ)设 ,若数列
,若数列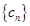 是单调递减数列,求实数
是单调递减数列,求实数 的取值范围.
的取值范围.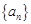 中,
中,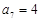 ,
,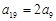 .
.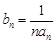 ,求数列
,求数列 的前
的前 项和
项和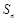 .
.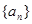 的前n项和为
的前n项和为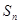 ,且
,且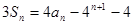
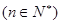 ,令
,令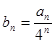 .
.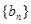 是等差数列,并求数列
是等差数列,并求数列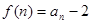
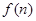 是18的倍数.
是18的倍数.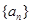 的公差为
的公差为 ,点
,点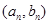 在函数
在函数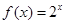 的图象上(
的图象上( ).
).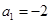 ,点
,点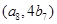 在函数
在函数 的图象上,求数列
的图象上,求数列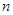 项和
项和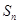 ;
;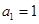 ,学科网函数
,学科网函数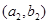 处的切线在
处的切线在 轴上的截距为
轴上的截距为 ,求数列
,求数列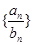 的前
的前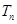 .
.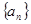 满足:
满足: ,
,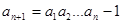 (
(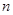 ≥3),记
≥3),记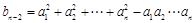
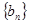 为等差数列,并求通项公式;
为等差数列,并求通项公式; ,数列{
,数列{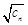 }的前n项和为
}的前n项和为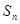 ,求证:
,求证: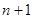 .
.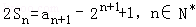 ,且a1,a2+5,a3成等差数列.
,且a1,a2+5,a3成等差数列.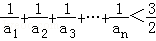 .
.