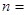题目内容
已知公差不为0的等差数列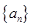 满足
满足 ,
,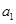 ,
,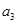 ,
,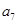 成等比数列.
成等比数列.
(1)求数列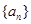 的通项公式;(2)数列
的通项公式;(2)数列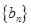 满足
满足 ,求数列
,求数列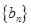 的前
的前 项和
项和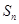 ;(Ⅲ)设
;(Ⅲ)设 ,若数列
,若数列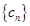 是单调递减数列,求实数
是单调递减数列,求实数 的取值范围.
的取值范围.
(1)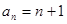 ;(2)
;(2)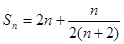 ;(3)
;(3)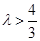 .
.
解析试题分析:(1)由等差数列的通项公式可将条件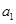 ,
,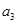 ,
,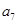 成等比数列,转化为关于公差的方程,解此方程求得公差值,从而就可写出其通项公式;(2)由(1)的结果可求得数列
成等比数列,转化为关于公差的方程,解此方程求得公差值,从而就可写出其通项公式;(2)由(1)的结果可求得数列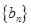 的通项公式,发现其前n项和可用裂项相消求和法解决;(3)数列
的通项公式,发现其前n项和可用裂项相消求和法解决;(3)数列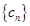 是单调递减数列,等价于
是单调递减数列,等价于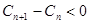 对
对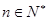 都成立,将(1)的结果代入,然后将参数
都成立,将(1)的结果代入,然后将参数 分离出来,可转化为研究一个新数列的最大项问题,对此新数列再用比差法研究其单调性,进而就可求得其最大项,从而获得
分离出来,可转化为研究一个新数列的最大项问题,对此新数列再用比差法研究其单调性,进而就可求得其最大项,从而获得 的取值范围.
的取值范围.
试题解析:(1)由题知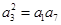 ,设
,设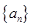 的公差为
的公差为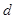 ,则
,则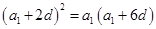 ,
,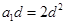 ,
,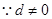

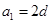 .
. 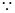


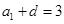
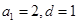
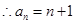 .
.
(2)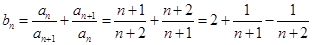 .
. 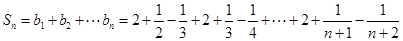
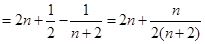 .
.
(3)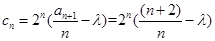 ,使数列
,使数列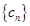 是单调递减数列,
是单调递减数列,
则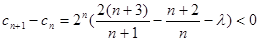 对
对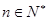 都成立
都成立
即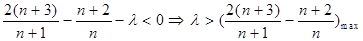
设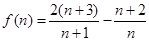
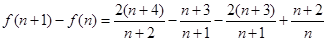
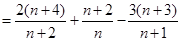
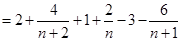
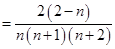
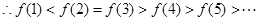
当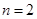 或
或 时,
时,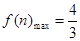 所以
所以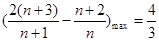 所以
所以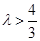 .
.
考点:1.等差数列与等比数列;2.数列的单调性;3.不等式的恒成立.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 为等差数列,且
为等差数列,且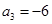 ,
,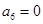 .
. 满足
满足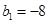 ,
, ,求
,求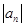 ,
, 。
。 的前
的前 项和为
项和为 且
且 .
. 的通项公式为
的通项公式为 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得
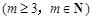 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由. 的前n项和为
的前n项和为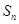 ,若
,若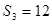 ,且
,且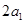 ,
,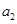 ,
,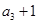 成等比数列,
成等比数列,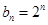 ,求数列
,求数列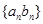 的前n项和
的前n项和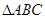 中,角
中,角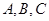 的对边分别为
的对边分别为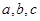 ,且
,且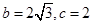 ,求
,求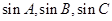 成等比数列,试判断
成等比数列,试判断 的等差数列,已知它的前10项和为
的等差数列,已知它的前10项和为 ,且a1,a2,a4 成等比数列.
,且a1,a2,a4 成等比数列.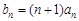 ,求数列
,求数列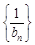 的前
的前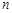 项和Tn .
项和Tn .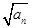 ,an+1)( n ∈N*)在函数y=x2+1的图象上.
,an+1)( n ∈N*)在函数y=x2+1的图象上.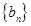 满足b1=1,
满足b1=1,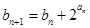 ,求证:
,求证: .
. 为等差数列,若
为等差数列,若 ,且它的前
,且它的前 项和
项和 有最小值,那么当
有最小值,那么当