题目内容
【题目】如图，已知A，B两镇分别位于东西湖岸MN的A处和湖中小岛的B处，点C在A的正西方向1 km处，tan∠BAN＝
，∠BCN＝
，.现计划铺设一条电缆连通A，B两镇，有两种铺设方案：①沿线段AB在水下铺设；②在湖岸MN上选一点P，先沿线段AP在地下铺设，再沿线段PB在水下铺设，预算地下、水下的电缆铺设费用分别为2万元km、4万元km.
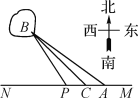
（1）求A，B两镇间的距离；
（2）应该如何铺设，使总铺设费用最低？
【答案】（1）5km（2）点P选在A镇的正西方向(4－
) km处，总铺设费用最低
【解析】
（1）过B作MN的垂线，垂足为D，在Rt△ABD和Rt△BCD中利用正切的定义表示AD，CD，借助AC＝AD－CD构建方程，求得BD，AD，进而由勾股定理，得答案；
（2）方案①总费用等于单价乘以长度；方案②：设∠BPD＝θ，在Rt△BDP中利用正弦函数和正切函数的定义用θ表示BP,AP长度，进而构建总铺设费用的函数，利用导数分析该函数的单调性，得此方案的最小值；最后比较方案①和方案②的费用，确定答案.
（1） 如图，过B作MN的垂线，垂足为D.
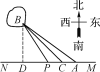
在Rt△ABD中，tan∠BAD＝tan∠BAN＝
＝
，
所以AD＝
BD.
在Rt△BCD中，tan∠BCD＝tan∠BCN＝
＝1，
所以CD＝BD.
则AC＝AD－CD＝BD－BD＝
BD＝1，
所以BD＝3，则CD＝3，AD＝4.
由勾股定理得，AB＝
＝5(km)．
所以A，B两镇间的距离为5km
（2） 方案①：沿线段AB在水下铺设时，总铺设费用为5×4＝20(万元)
方案②：设∠BPD＝θ，则θ∈
，其中θ0＝∠BAN.
在Rt△BDP中，DP＝
，BP＝
，
所以AP＝4－DP＝4－
.
则总铺设费用为2AP＋4BP＝8－
设f(θ)＝
，则f′(θ)＝
，
令f′(θ)＝0，得
即θ＝
，列表如下：
θ |
|
|
|
f′(θ) | － | 0 | ＋ |
f(θ) | 单调递减 | 极小值 | 单调递增 |
所以f(θ)的最小值为
.
所以方案②的总铺设费用最低为
(万元)，此时AP＝4－
.
而
，所以应选择方案②进行铺设，点P选在A镇的正西方向(4－) km处，总铺设费用最低．
