题目内容
【题目】已知函数f(x)![]() 若方程2[f(x)]2﹣5tf(x)+3t2=0恰有4个不同的实根,则实数t的取值范围为(参考数据:ln2≈0.6931)( )
若方程2[f(x)]2﹣5tf(x)+3t2=0恰有4个不同的实根,则实数t的取值范围为(参考数据:ln2≈0.6931)( )
A.(![]() ,
,![]() )
)
B.(![]() ,
,![]() )
)
C.(![]() ,2﹣2ln2)∪(
,2﹣2ln2)∪(![]() ,1)
,1)
D.(![]() ,2﹣1n2)
,2﹣1n2)
【答案】C
【解析】
由![]() ,得
,得![]() ,或
,或![]() ,当
,当![]() ,对
,对![]() 求导,求出单调区间极值,作出
求导,求出单调区间极值,作出![]() 草图,根据图像求出
草图,根据图像求出![]() 与
与![]() 的交点情况,结合方程有4个解,求出
的交点情况,结合方程有4个解,求出![]() 的范围,即可求解.
的范围,即可求解.
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 的递减区间是
的递减区间是![]() ,
,
递增区间是![]() 时,
时,![]() 取得极小值为
取得极小值为![]() ,
,
![]() 在
在![]() 单调递增,
单调递增,
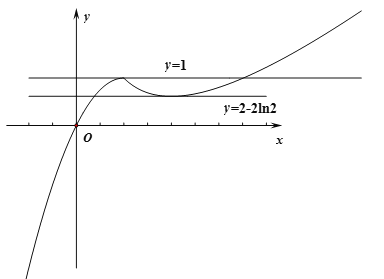
作出函数![]() 图像,如下图所示:
图像,如下图所示:
当![]() 或
或![]() 时,
时,![]() 有一个实根,
有一个实根,
当![]() 或
或![]() 时,
时,![]() 有两个实根,
有两个实根,
当![]() 时,
时,![]() 有三个实根,
有三个实根,
由![]() ,得
,得![]() ,或
,或![]() ,
,
方程有四个实根, 所以![]() ,
,
![]() ,
,![]() ,有四个实根,有以下情况:
,有四个实根,有以下情况:
![]()
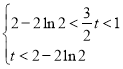 解得
解得![]() ;
;
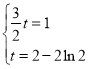 ,
,![]() 不存在;
不存在;
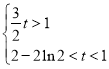 ,解得
,解得![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .
.
故选:C

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目