题目内容
【题目】设曲线E的方程为![]() 1,动点A(m,n),B(﹣m,n),C(﹣m,﹣n),D(m,﹣n)在E上,对于结论:①四边形ABCD的面积的最小值为48;②四边形ABCD外接圆的面积的最小值为25π.下面说法正确的是( )
1,动点A(m,n),B(﹣m,n),C(﹣m,﹣n),D(m,﹣n)在E上,对于结论:①四边形ABCD的面积的最小值为48;②四边形ABCD外接圆的面积的最小值为25π.下面说法正确的是( )
A.①错,②对B.①对,②错C.①②都错D.①②都对
【答案】D
【解析】
根据点的对称性可知四边形ABCD是矩形,结合矩形的面积公式和外接圆的面积公式可求.
因为动点A(m,n),B(﹣m,n),C(﹣m,﹣n),D(m,﹣n),所以四边形ABCD是矩形;
不妨设![]() ,则矩形ABCD的面积为
,则矩形ABCD的面积为![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时等号成立;
时等号成立;
所以矩形ABCD的面积最小值为48.
四边形ABCD外接圆的直径为![]() ,
,
所以四边形ABCD外接圆的面积为![]() ,
,
因为![]() ,所以
,所以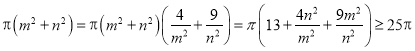 ,当且仅当
,当且仅当![]() 时等号成立;
时等号成立;
故选:D.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目