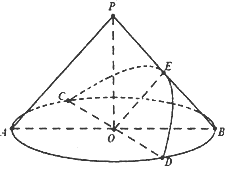
题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）的离心率为 
，椭圆C的长轴长为4．
（1）求椭圆C的方程；
（2）已知直线l：y=kx+ 
与椭圆C交于A，B两点，是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O？若存在，求出k的值；若不存在，请说明理由．
【答案】
（1）解：设椭圆的焦半距为c，则由题设，得：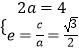 
，
解得 
所以b2=a2﹣c2=4﹣3=1，
故所求椭圆C的方程为 
+x2=1．
（2）解：存在实数k使得以线段AB为直径的圆恰好经过坐标原点O．
理由如下：
设点A（x1，y1），B（x2，y2），
将直线l 的方程y=kx+ 
代入 +x2=1，
并整理，得（k2+4）x2+2 kx﹣1=0．（*）
则x1+x2=﹣ 
，x1x2=﹣ 
．
因为以线段AB为直径的圆恰好经过坐标原点O，
所以 
=0，即x1x2+y1y2=0．
又y1y2=k2x1x2+ k（x1+x2）+3，
于是﹣ 
﹣ 
+3=0，解得k=± 
，
经检验知：此时（*）式的△＞0，符合题意．
所以当k=± 时，以线段AB为直径的圆恰好经过坐标原点O．
【解析】（1）设椭圆的焦半距为c，则由题设，得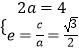： ，解得a，b，c值，可得椭圆C的方程；（2）设点A（x1 ， y1），B（x2 ， y2），将直线l 的方程y=kx+ 代入 +x2=1，利用韦达定理，及向量垂直的充要条件，可求出满足条件的k值．
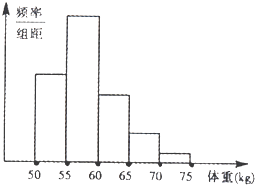
【题目】长春市的“名师云课”活动自开展以来获得广大家长和学子的高度赞誉，在我市推出的第二季名师云课中，数学学科共计推出36节云课，为了更好地将课程内容呈现给广大学子，现对某一时段云课的点击量进行统计：
点击量 |
|
|
|
节数 | 6 | 18 | 12 |
（Ⅰ）现从36节云课中采用分层抽样的方式选出6节，求选出的点击量超过3000的节数．
（Ⅱ）为了更好地搭建云课平台，现将云课进行剪辑，若点击量在区间
内，则需要花费40分钟进行剪辑，若点击量在区间
内，则需要花费20分钟进行剪辑，点击量超过3000，则不需要剪辑，现从（Ⅰ）中选出的6节课中任意取出2节课进行剪辑，求剪辑时间为40分钟的概率．
