题目内容
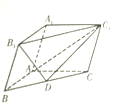
【题目】某几何体的三视图的形状、大小如图所示． 
（1）求该几何体的体积；
（2）设点D、E分别在线段AC、BC上，且DE∥平面ABB1A1 ， 求证：DE∥A1B1 ．
【答案】
（1）由三视图可以看出，此几何体是一个三棱柱，其高为3，底面是一个腰为2，底为2 的等腰三角形，
∴底面三角形的高为
∴体积为3× × × =6
（2）证明：设点D、E分别在线段AC、BC上，且DE∥平面ABB1A1，
∵面ABC∩平面ABB1DE∥A1B1A1=AB
∴DE∥AB，由三棱柱的性质知AB∥B1A1，
∴DE∥A1B1
【解析】分析：（1）求该几何体的体积，由三视图可以看出，此几何体是一个三棱柱，其高为3，底面是一个腰为2，底为2 
的等腰三角形，由此不难求出体积；（2）由于DE∥平面ABB1A1 ， 故直接用线面平行的性质定理即可得出DE∥AB，再由平行的传递性即可得到所证的结论．
【考点精析】利用直线与平面平行的性质对题目进行判断即可得到答案，需要熟知一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行．
练习册系列答案
相关题目
