题目内容
13．在△ABC中，A=45°，AB=2，BC=3，则AC=$\sqrt{2}+\sqrt{7}$．分析 由已知及余弦定理可得AC2-2$\sqrt{2}$AC-5=0，即可解得AC的值．
解答 解：∵A=45°，AB=2，BC=3，
∴由余弦定理可得：BC2=AC2+AB2-2AC•ABcosC，既有：9=AC2+4-4ACcos45°，可得：AC2-2$\sqrt{2}$AC-5=0，
∴可解得：AC=$\sqrt{2}-\sqrt{7}$（舍去），或AC=$\sqrt{2}+\sqrt{7}$，
故答案为：$\sqrt{2}+\sqrt{7}$．
点评 本题主要考查了余弦定理的应用，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
13．已知集合P={x|x2-2x≥3}，Q={x|2＜x＜4}，则P∩Q=（ ）
| A． | [3，4） | B． | （2，3] | C． | （-1，2） | D． | （-1，3] |
18．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的焦点到其渐近线的距离等于4，抛物线y2=2px的焦点为双曲线的右焦点，双曲线截抛物线的准线所得的线段长为8，则抛物线方程为（ ）
| A． | y2=4x | B． | y2=4$\sqrt{2}x$ | C． | y2=8$\sqrt{2}x$ | D． | y2=16$\sqrt{2}x$ |
2．已知函数f（x）=$\frac{{e}^{x}-{e}^{-x}}{2}$，x∈R，若对任意θ∈（0，$\frac{π}{2}$]，都有f（sinθ）+f（1-m）＞0成立，则实数m的取值范围是（ ）
| A． | （0，1） | B． | （0，2） | C． | （-∞，1） | D． | （-∞，1] |
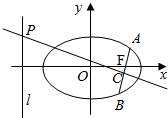如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且右焦点F到左准线l的距离为3．