题目内容
2.已知函数f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,x∈R,若对任意θ∈(0,$\frac{π}{2}$],都有f(sinθ)+f(1-m)>0成立,则实数m的取值范围是( )| A. | (0,1) | B. | (0,2) | C. | (-∞,1) | D. | (-∞,1] |
分析 求函数f(x)定义域,及f(-x)便得到f(x)为奇函数,并能够通过求f′(x)判断f(x)在R上单调递增,从而得到sinθ>m-1,也就是对任意的$θ∈(0,\frac{π}{2}]$都有sinθ>m-1成立,根据0<sinθ≤1,即可得出m的取值范围.
解答 解:f(x)的定义域为R,f(-x)=-f(x);
f′(x)=ex+e-x>0;
∴f(x)在R上单调递增;
由f(sinθ)+f(1-m)>0得,f(sinθ)>f(m-1);
∴sinθ>m-1;
即对任意θ∈$(0,\frac{π}{2}]$都有m-1<sinθ成立;
∵0<sinθ≤1;
∴m-1≤0;
∴实数m的取值范围是(-∞,1].
故选D.
点评 考查奇函数的定义,根据函数导数判断函数单调性的方法,复合函数的求导公式,以及函数单调性定义的运用,正弦函数的值域.

练习册系列答案
相关题目
12.若正数a,b满足2+log2a=3+log3b=log6(a+b),则$\frac{1}{a}$+$\frac{1}{b}$的值为( )
| A. | 36 | B. | 72 | C. | 108 | D. | $\frac{1}{72}$ |
7.设i是虚数单位,复数z满足(z+i)(1-i)=-2i,则z的共轭复数$\overline{z}$=( )
| A. | 1+2i | B. | 1-2i | C. | 2+i | D. | 2-i |
 在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,斜截圆柱的截面是一个椭圆,则该椭圆的焦距为30cm.
在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,斜截圆柱的截面是一个椭圆,则该椭圆的焦距为30cm. ,那么数列
,那么数列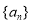 是( )
是( )