题目内容
20.已知O是正三角形ABC内部一点,$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$,在三角形ABC内随机撒一粒黄豆,落在三角形AOC内的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
分析 由$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$变形为$\overrightarrow{OA}$+3$\overrightarrow{OC}$=-2$\overrightarrow{OB}$.以$\overrightarrow{OA}$、3$\overrightarrow{OC}$所在的线段OA、OE为邻边作平行四边形OAFE.
设对角线OF与AC交与点D.利用向量的平行四边形法则和平行四边形的性质可得$\frac{OD}{BD}$=$\frac{1}{3}$,△AOC与△ABC的面积的比值=$\frac{1}{3}$.进而得出在三角形ABC内随机撒一粒黄豆,落在三角形AOC内的概率.
解答 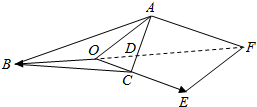 解:如图所示,
解:如图所示,
由$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$变形为$\overrightarrow{OA}$+3$\overrightarrow{OC}$=-2$\overrightarrow{OB}$.
以$\overrightarrow{OA}$、3$\overrightarrow{OC}$所在的线段OA、OE为邻边作平行四边形OAFE.
设对角线OF与AC交与点D.
则$\overrightarrow{OF}$=-2$\overrightarrow{OB}$.
∴$\frac{OD}{DF}=\frac{OC}{AF}=\frac{1}{3}$,
∴$\frac{OD}{2OB-OD}$=$\frac{1}{3}$,化为$\frac{OD}{OB}$=$\frac{1}{2}$,即$\frac{OD}{BD}$=$\frac{1}{3}$.
∴△AOC与△ABC的面积的比值=$\frac{1}{3}$.
∴在三角形ABC内随机撒一粒黄豆,落在三角形AOC内的概率为$\frac{1}{3}$.
故选:B.
点评 本题考查了向量的平行四边形法则和平行四边形的性质,考查了作辅助线的重要性和技巧,属于难题.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | 对于命题p:?x∈R,使得x2+x+1<0,则¬p为:?x∈R,均有x2+x+1≥0 | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | “x>2”是“x2-3x+2>0”的充分不必要条件 |

| A. | AD•AB=CD2 | B. | CE•CB=AD•AB | C. | CE•CB=AD•DB | D. | CE•EB=CD2 |
| A. | 90 | B. | 80 | C. | 100 | D. | 120 |
| A. | 20 | B. | 16 | C. | -18 | D. | -17 |