题目内容
已知F1、F2为双曲线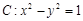 的左、右焦点,点P在C上,
的左、右焦点,点P在C上,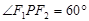 ,则P到x轴的距离为 ( )
,则P到x轴的距离为 ( )
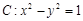 的左、右焦点,点P在C上,
的左、右焦点,点P在C上,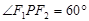 ,则P到x轴的距离为 ( )
,则P到x轴的距离为 ( )A.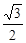 | B.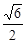 | C.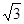 | D.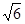 |
B
试题分析:由余弦定理得
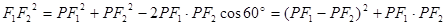 ,所以
,所以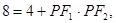 即
即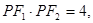 由三角形面积得
由三角形面积得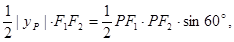 解得
解得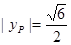 ,因此P到x轴的距离为
,因此P到x轴的距离为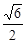 .
. 
练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
题目内容
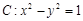 的左、右焦点,点P在C上,
的左、右焦点,点P在C上,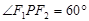 ,则P到x轴的距离为 ( )
,则P到x轴的距离为 ( )A.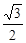 | B.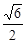 | C.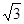 | D.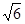 |
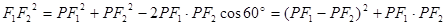 ,所以
,所以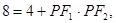 即
即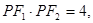 由三角形面积得
由三角形面积得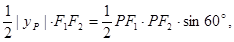 解得
解得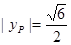 ,因此P到x轴的距离为
,因此P到x轴的距离为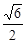 .
. 
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案