题目内容
【题目】已知椭圆的中心在原点,焦点在x轴上![]() 分别为左、右焦点,椭圆的一个顶点与两焦点构成等边三角形,且
分别为左、右焦点,椭圆的一个顶点与两焦点构成等边三角形,且![]() .
.
(1)求椭圆方程;
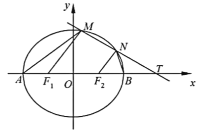
(2)对于x轴上的某一点T,过T作不与坐标轴平行的直线L交椭圆于![]() 两点,若存在x轴上的点S,使得对符合条件的L恒有
两点,若存在x轴上的点S,使得对符合条件的L恒有![]() 成立,我们称S为T的一个配对点,当T为左焦点时,求T的配对点的坐标;
成立,我们称S为T的一个配对点,当T为左焦点时,求T的配对点的坐标;
(3)在(2)条件下讨论当T在何处时,存在有配对点?
【答案】(1)![]() (2)(-4,0)(3)
(2)(-4,0)(3)![]()
【解析】
(1)设椭圆的顶点为P,由![]() 可得
可得![]() ,由
,由![]() 结合椭圆的定义可得2a,结合
结合椭圆的定义可得2a,结合![]() 可求椭圆的方程
可求椭圆的方程
(2)可设过T的直线方程为![]() ,
,![]() ,联立椭圆方程整理可得
,联立椭圆方程整理可得![]() ,设
,设![]() ,
,![]() ,
,![]() ,由
,由![]() 得
得![]() 即
即![]() ,结合方程的根与系数的关系代入可求a
,结合方程的根与系数的关系代入可求a
(3)设![]() ,直线
,直线![]() 的方程
的方程![]() ,
,![]() ,使得对符合条件的L恒有
,使得对符合条件的L恒有![]() 成立,则T必须在
成立,则T必须在![]() 之间即
之间即![]()
同(2)的整理方法,联立直线与椭圆方程由![]() 可得,
可得,![]() ,同(2)的方法一样代入可求
,同(2)的方法一样代入可求
解:(1)设椭圆的顶点为P,由![]() 可得
可得![]()
![]() 可得
可得![]()
![]() ,
,![]()
椭圆的方程为:![]()
(2)![]() ,
,
则过可设过T的直线方程为![]() ,
,![]() ,
,
联立椭圆方程整理可得![]()
设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]()
![]()
![]()
![]()
整理可得![]()
即![]()
![]()
(3)设![]() ,直线
,直线![]() 的方程
的方程![]() ,
,![]()
使得对符合条件的L恒有![]() 成立,则T必须在
成立,则T必须在![]() 之间即
之间即![]()
同(2)的整理方法,联立直线与椭圆方程可得,![]() ,
,![]()
由![]() 可得,
可得,![]()
同(2)的方法一样代入可求![]() .
.

【题目】当前,旅游已经成为新时期人民群众美好生活和精神文化需求的重要内容.旅游是综合性产业,是拉动经济发展的重要动力,也为整个经济结构调整注入活力.文化旅游产业研究院发布了《2019年中国文旅产业发展趋势报告》,报告指出:旅游业稳步增长,每年占国家GDP总量的比例逐年增加,如图及下表为2014年到2018年的相关统计数据.
旅游收入占国家GDP总量比例趋势 | |||||
年份: | 1 | 2 | 3 | 4 | 5 |
占比: | 10.4 | 10.8 | 11.0 | 11.0 | 11.2 |
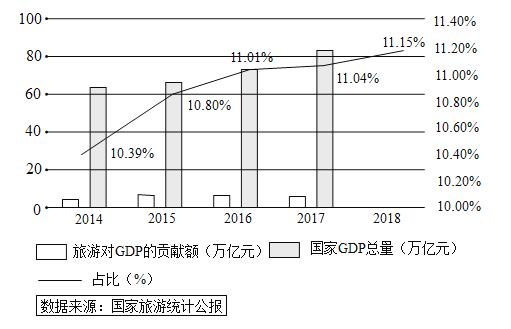
(1)根据以上数据,求出占比![]() 关于年份
关于年份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)所求线性回归方程,预测2019年的旅游收入所占的比例.
附: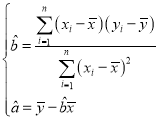 .
.