Question

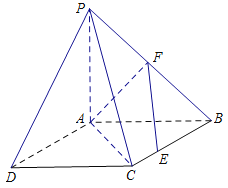
【题目】如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，则下列结论中：①PB⊥AE；②平面ABC⊥平面PBC；③直线BC∥平面PAE；④∠PDA=45°.

其中正确的有____________(把所有正确的序号都填上).

Answer 1

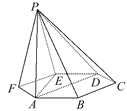
【答案】①④

【解析】对于①，因为PA⊥平面ABC，所以PA⊥AE，又，所以平面PAB，从而可得，故①正确。

对于②，由于PA⊥平面ABC，所以平面ABC与平面PBC不可能垂直，故②不正确。

对于③，由于在正六边形中，所以BC与EA必有公共点，从而BC与平面PAE有公共点，所以直线BC与平面PAE不平行，故③不正确。

对于④，由条件得为直角三角形，且PA⊥AD，又，所以∠PDA=45°。故④正确。

综上①④正确。

答案：①④