Question

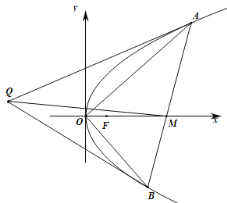
【题目】如图，已知直线与抛物线相交于两点，为坐标原点，直线与轴相交于点，且.

（1）求证:；

（2）求点的横坐标；

（3）过点分别作抛物线的切线，两条切线交于点，求.

Answer 1

【答案】（1）证明见解析；（2）；（3）.

【解析】

（1）设直线的方程为：，代入抛物线,运用韦达定理，结合条件，再由斜率数量积垂直的性质，即可证明；

（2）由直线，令，可得的横坐标；

（3）求出抛物线上的点的切线的斜率和方程，求出点的坐标，再由直线的斜率公式可得答案.

证明：（1）设直线的方程为：，代入抛物线，

可得：，由，，

可得，，，

由，可得，

可得,即：；

（2）由直线，令，可得，

即点的横坐标为：；

（3）由，两边对求导，可得，即，

可得处切线的斜率为，切线方程为：，

由，，可得 ①

同理可得：处切线方程为 ②

由①②可得：，

，

故，

可得：.