题目内容
15.已知中心在原点,焦点在坐标轴上的双曲线与圆x2+y2=5有公共点A(1,2),且圆在A点的切线与双曲线的渐近线平行,则双曲线的离心率为$\frac{\sqrt{5}}{2}$.分析 求出圆的切线方程,利用圆在A点的切线与双曲线的渐近线平行关系,推出双曲线的离心率.
解答 解:圆x2+y2=5有公共点A(1,2),KOA=2,圆在A点的切线方程的斜率为:$-\frac{1}{2}$,
圆在A点的切线为:y-2=-$\frac{1}{2}$(x-1),即x+2y-5=0,
圆在A点的切线与双曲线的渐近线平行,并且中心在原点,焦点在坐标轴上的双曲线,
可得$\frac{b}{a}=\frac{1}{2}$,∴$\frac{{c}^{2}-{a}^{2}}{{a}^{2}}=\frac{1}{4}$,可得e2=$\frac{5}{4}$,e=$\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题看双曲线与圆的位置关系,双曲线的离心率的求法,圆的切线方程的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)在[0,1]上递增”是“f(x)在[1,2]上递减”的( )
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 充分而不必要条件 |
10.“a=0”是“函数y=(x+a)2是偶函数”的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
20.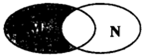 已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )
已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )
 已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )
已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )| A. | {x|0<x<1} | B. | {x|0<x≤1} | C. | {x|1<x<2} | D. | {x|2<x<3} |
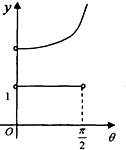
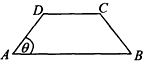 如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,$\frac{π}{2}$),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,设e1=f(θ),e1e2=g(θ),则f(θ),g(θ)的大致图象是( )
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,$\frac{π}{2}$),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,设e1=f(θ),e1e2=g(θ),则f(θ),g(θ)的大致图象是( )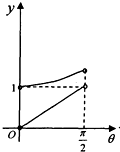
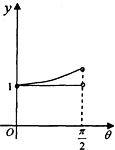

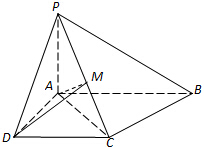 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.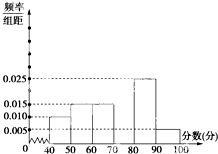 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: