题目内容
在正方体ABCD—A1B1C1D1中,M、N、P、Q分别是棱AB、BC、CD、CC1的中点,直线MN与PQ所成的度数是( )
A. B.
B.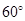 C.
C. D.
D.
B
解析试题分析:在正方体ABCD—A1B1C1D1中,连接AB1,AC,B1C,因为M、N、P、Q分别是棱AB、BC、CD、CC1的中点,所以MN//AC,PQ//C1D//AB1,所以∠CAB1即为异面直线MN与PQ所成的角,因为∆AB1C为等边三角形,所以∠CAB1=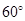 。
。
考点:异面直线所成的角。
点评:本题主要考查异面直线所成的角,对于异面直线所成的角我们可以通过平移直线得到。但我们要一定要注意异面直线所成角的范围: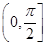 。
。

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为( )
| A.75° | B.60° | C.45° | D.30° |
已知 、
、 、
、 是三条不同的直线,
是三条不同的直线, 、
、 、
、 是三个不同的平面,给出以下命题:
是三个不同的平面,给出以下命题:
①若 ,则
,则 ; ②若
; ②若 ,则
,则 ;③若
;③若 ,
, ,则
,则 ;④若
;④若 ,
, ,则
,则 .
.
其中正确命题的序号是( )
| A.②④ | B.②③ | C.③④ | D.①③ |
如图所示,在棱长为2的正方体 内(含正方体表面)任取一点
内(含正方体表面)任取一点 ,则
,则 的概率
的概率 ( )
( ) 
A. | B. | C. | D. |
已知 、
、 是不同的平面,
是不同的平面, 、
、 是不同的直线,则下列命题不正确的( )
是不同的直线,则下列命题不正确的( )
A.若 ∥ ∥ 则 则 | B.若 ∥ ∥ 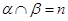 ,则 ,则 ∥ ∥ |
C.若 ∥ ∥ , , ,则 ,则 | D.若  则 则 ∥ ∥ |
已知 是两个不同的平面,
是两个不同的平面, 是不同的直线,下列命题不正确的是
是不同的直线,下列命题不正确的是
A.若 则 则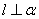 |
B.若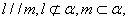 则 则 |
C.若 则 则 |
D.若 ,则 ,则 |
设 为两条直线,
为两条直线,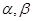 为两个平面,则下列结论成立的是( )
为两个平面,则下列结论成立的是( )
A.若 且 且 ,则 ,则 | B.若 且 且 ,则 ,则 |
C.若 , , 则 则 | D.若 则 则 |
已知m,n是两条不重合的直线, 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题:
①若m
 ,m
,m
 ,则
,则 ∥
∥ ; ②若
; ②若

 ,
,

 则
则 ∥
∥
③若m// ,n //
,n // ,m//n 则
,m//n 则 //
// ④若m
④若m
 ,m//
,m// ,则
,则


其中真命题是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
 ,则这个二面角的大小为( )
,则这个二面角的大小为( )



