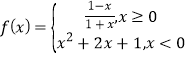题目内容
【题目】已知函数![]() ,函数
,函数![]() ,其中
,其中![]() ,
,![]() 是
是![]() 的一个极值点,且
的一个极值点,且![]() .
.
(1)讨论![]() 的单调性
的单调性
(2)求实数![]() 和a的值
和a的值
(3)证明![]()
【答案】(1)![]() 在区间
在区间![]() 单调递增;(2)
单调递增;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)求出![]() ,在定义域内,再次求导,可得在区间
,在定义域内,再次求导,可得在区间![]() 上
上![]() 恒成立,从而可得结论;(2)由
恒成立,从而可得结论;(2)由![]() ,可得
,可得![]() ,由
,由![]() 可得
可得![]() ,联立解方程组可得结果;(3)由(1)知
,联立解方程组可得结果;(3)由(1)知![]() 在区间
在区间![]() 单调递增,可证明
单调递增,可证明![]() ,取
,取![]() ,可得
,可得![]() ,而
,而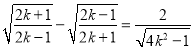 ,利用裂项相消法,结合放缩法可得结果.
,利用裂项相消法,结合放缩法可得结果.
(1)由已知可得函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
令![]() ,则有
,则有![]() ,由
,由![]() ,可得
,可得![]() ,
,
可知当x变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
| 1 |
|
| - | 0 | + |
|
| 极小值 |
|
![]() ,即
,即![]() ,可得
,可得![]() 在区间
在区间![]() 单调递增;
单调递增;
(2)由已知可得函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
由已知得![]() ,即
,即![]() ,①
,①
由![]() 可得,
可得,![]() ,②
,②
联立①②,消去a,可得![]() ,③
,③
令![]() ,则
,则![]() ,
,
由(1)知,![]() ,故
,故![]() ,
,![]() 在区间
在区间![]() 单调递增,
单调递增,
注意到![]() ,所以方程③有唯一解
,所以方程③有唯一解![]() ,代入①,可得
,代入①,可得![]() ,
,
![]() ;
;
(3)证明:由(1)知![]() 在区间
在区间![]() 单调递增,
单调递增,
故当![]() 时,
时,![]() ,
,![]() ,
,
可得![]() 在区间
在区间![]() 单调递增,
单调递增,
因此,当![]() 时,
时,![]() ,即
,即![]() ,亦即
,亦即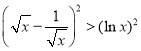 ,
,
这时![]() ,故可得
,故可得![]() ,取
,取![]() ,
,
可得![]() ,而
,而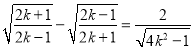 ,
,
故![]()
![]() .
.

【题目】近几年一种新奇水果深受广大消费者的喜爱,一位农户发挥聪明才智,把这种露天种植的新奇水果搬到了大棚里,收到了很好的经济效益.根据资料显示,产出的新奇水果的箱数x(单位:十箱)与成本y(单位:千元)的关系如下:
x | 1 | 3 | 4 | 6 | 7 |
y | 5 | 6.5 | 7 | 7.5 | 8 |
y与x可用回归方程![]() ( 其中
( 其中![]() ,
,![]() 为常数)进行模拟.
为常数)进行模拟.
(Ⅰ)若该农户产出的该新奇水果的价格为150元/箱,试预测该新奇水果100箱的利润是多少元.|.
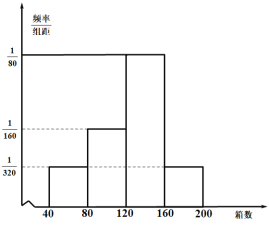
(Ⅱ)据统计,10月份的连续16天中该农户每天为甲地配送的该新奇水果的箱数的频率分布直方图如图所示.
(i)若从箱数在![]() 内的天数中随机抽取2天,估计恰有1天的水果箱数在
内的天数中随机抽取2天,估计恰有1天的水果箱数在![]() 内的概率;
内的概率;
(ⅱ)求这16天该农户每天为甲地配送的该新奇水果的箱数的平均值.(每组用该组区间的中点值作代表)
参考数据与公式:设![]() ,则
,则
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
线性回归直线![]() 中,
中,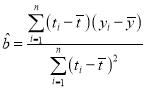 ,
,![]() .
.
【题目】某鲜花批发店每天早晨以每支2元的价格从鲜切花生产基地购入某种玫瑰,经过保鲜加工后全部装箱(每箱500支,平均每支玫瑰的保鲜加工成本为1元),然后以每箱2000元的价格整箱出售.由于鲜花的保鲜特点,制定了如下促销策略:若每天下午3点以前所购进的玫瑰没有售完,则对未售出的玫瑰以每箱1200元的价格降价处理.根据经验,降价后能够把剩余玫瑰全部处理完毕,且当天不再购进该种玫瑰.因库房限制每天最多加工6箱.
(1)若某天此鲜花批发店购入并加工了6箱该种玫瑰,在下午3点以前售出4箱,且6箱该种玫瑰被6位不同的顾客购买.现从这6位顾客中随机选取2人赠送优惠卡,求恰好一位是以2000元价格购买的顾客且另一位是以1200元价格购买的顾客的概率:
(2)此鲜花批发店统计了100天该种玫瑰在每天下午3点以前的销售量t(单位:箱),统计结果如下表所示(视频率为概率):
t/箱 | 4 | 5 | 6 |
频数 | 30 | x | s |
①估计接下来的一个月(30天)该种玫瑰每天下午3点前的销售量不少于5箱的天数并说明理由;
②记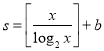 ,
,![]() ,若此批发店每天购进的该种玫瑰箱数为5箱时所获得的平均利润最大,求实数b的最小值(不考虑其他成本,
,若此批发店每天购进的该种玫瑰箱数为5箱时所获得的平均利润最大,求实数b的最小值(不考虑其他成本,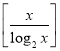 为
为![]() 的整数部分,例如:
的整数部分,例如:![]() ,
,![]() ).
).