题目内容
(本题满分13分)
已知点 和互不相同的点
和互不相同的点 ,
,
满足 ,其中
,其中 分别为等差数列和等比数列,O为坐标原点,若
分别为等差数列和等比数列,O为坐标原点,若 为线段AB的中点。
为线段AB的中点。
(1)求 的值;
的值;
(2)证明 的公差为d =0,或
的公差为d =0,或 的公比为q=1,点
的公比为q=1,点 在同一直线上;
在同一直线上;
(3)若d 0,且q
0,且q  1,点
1,点 能否在同一直线上?证明你的结论
能否在同一直线上?证明你的结论
已知点
 和互不相同的点
和互不相同的点 ,
,满足
 ,其中
,其中 分别为等差数列和等比数列,O为坐标原点,若
分别为等差数列和等比数列,O为坐标原点,若 为线段AB的中点。
为线段AB的中点。(1)求
 的值;
的值;(2)证明
 的公差为d =0,或
的公差为d =0,或 的公比为q=1,点
的公比为q=1,点 在同一直线上;
在同一直线上;(3)若d
 0,且q
0,且q  1,点
1,点 能否在同一直线上?证明你的结论
能否在同一直线上?证明你的结论(1)
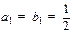
(2)证明略
(3)不在同一直线上,证明略
解:(1) 为线段AB
为线段AB 的中点
的中点 ,又
,又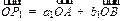 ,
,
且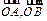 不共线,由平面向量的基本定理知
不共线,由平面向量的基本定理知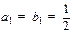 。
。
(2)由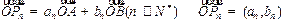 ,
,
设 的公差为d,
的公差为d, 的公比为q,则由于
的公比为q,则由于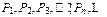 互不相同,
互不相同,
d=0,q=1所以不会同时成立。
若d=0,则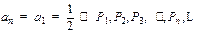 都在直线
都在直线 上;
上;
若q=1,则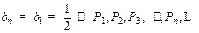 都在直线
都在直线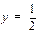 上;
上;
若d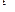 0,且q
0,且q 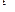 1,
1,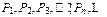 在同一直线上
在同一直线上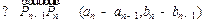 与
与
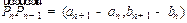 始终共线
始终共线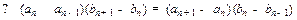
即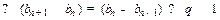 ,这与q
,这与q 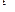 1矛盾。
1矛盾。
所以d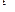 0,且q
0,且q 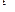 1,
1,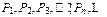 不可能在同一直线上
不可能在同一直线上
 为线段AB
为线段AB 的中点
的中点 ,又
,又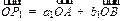 ,
,且
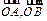 不共线,由平面向量的基本定理知
不共线,由平面向量的基本定理知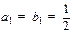 。
。(2)由
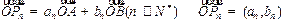 ,
,设
 的公差为d,
的公差为d, 的公比为q,则由于
的公比为q,则由于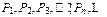 互不相同,
互不相同,d=0,q=1所以不会同时成立。
若d=0,则
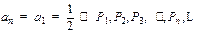 都在直线
都在直线 上;
上;若q=1,则
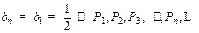 都在直线
都在直线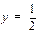 上;
上;若d
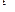 0,且q
0,且q 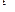 1,
1,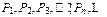 在同一直线上
在同一直线上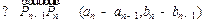 与
与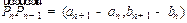 始终共线
始终共线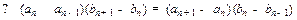
即
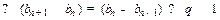 ,这与q
,这与q 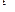 1矛盾。
1矛盾。所以d
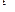 0,且q
0,且q 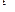 1,
1,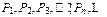 不可能在同一直线上
不可能在同一直线上
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目

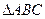 斜边BC的中线,用解析法证明
斜边BC的中线,用解析法证明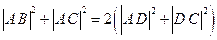 .
. 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设
 =
= ,
, 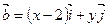
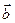 =,且满足
=,且满足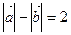
 过点
过点
 且法向量为
且法向量为 ,直线与轨迹
,直线与轨迹 交于
交于 两点.点
两点.点 ,无论直线
,无论直线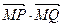 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数 的取值范围;(9分)
的取值范围;(9分)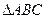 中角A的对边长等于2,向量
中角A的对边长等于2,向量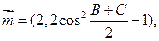 向量
向量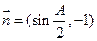 .
.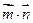 取最大值时,求角A的大小;
取最大值时,求角A的大小;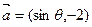 与
与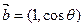 互相垂直,其中
互相垂直,其中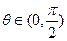 .
.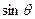 和
和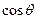 的值;
的值;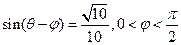 ,求
,求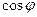 的值.
的值. 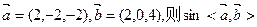 = 。
= 。 中,下列结论中正确的是( )
中,下列结论中正确的是( )
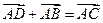
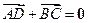
 在
在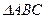 内部且满足
内部且满足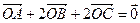 ,则
,则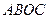 的面积之比为 .
的面积之比为 .