题目内容
已知两点M(-2,0),N(2,0),点P为坐标平面内的动点,且满足||||+·=0.
(1)求点P的轨迹C的方程;
(2)设过点N的直线l的斜率为k,且与曲线C相交于点S、T,若S、T两点只在第二象限内运动,线段ST的垂直平分线交x轴于Q点,求Q点横坐标的取值范围.
(1)求点P的轨迹C的方程;
(2)设过点N的直线l的斜率为k,且与曲线C相交于点S、T,若S、T两点只在第二象限内运动,线段ST的垂直平分线交x轴于Q点,求Q点横坐标的取值范围.
(1)设点P(x,y),根据题意则有:
=(4,0),||=4,
||=,=(x-2,y),
代入||||+·=0
得:4+4(x-2)=0.
整理得点P的轨迹C的方程:y2=-8x.
(2)设S(x1,y1),T(x2,y2),
由题意得:ST的方程为y=k(x-2)(显然k≠0)
与y2=-8x联立消元得:ky2+8y+16k=0,
则有:y1+y2=-,y1y2=16.
因为直线交轨迹C于两点,
则Δ=b2-4ac=64-64k2>0,
再由y1>0,y2>0,则->0,故-1<k<0.
可求得线段ST中点B的坐标为(-+2,-),
所以线段ST的垂直平分线方程为
y+=-(x+-2).
令y=0得点Q横坐标为xQ=-2-,
xQ=-2-<-6.
所以Q点横坐标的取值范围为(-∞,-6).
略

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
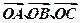 满足
满足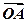 =[f(x
=[f(x )+2f′(1)]
)+2f′(1)]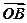 -ln(x+1)
-ln(x+1)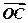 。
。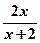 ;
;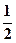 x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围。
x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围。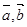 且
且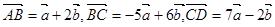 ,则一定共线的三点是
,则一定共线的三点是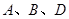
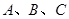
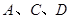
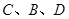
 和互不相同的点
和互不相同的点 ,
, ,其中
,其中 分别为等差数列和等比数列,O为坐标原点,若
分别为等差数列和等比数列,O为坐标原点,若 为线段AB的中点。
为线段AB的中点。 的值;
的值; 的公差为d =0,或
的公差为d =0,或 的公比为q=1,点
的公比为q=1,点 0,且q
0,且q 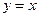 上动点,当|PA|+|PB|的值最小时,点P的坐标是
上动点,当|PA|+|PB|的值最小时,点P的坐标是 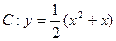 ,点
,点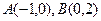 ,点E是曲线C上的一个动点(E不在直线AB上),设
,点E是曲线C上的一个动点(E不在直线AB上),设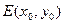 ,C,D在直线AB上,
,C,D在直线AB上,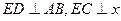 轴。
轴。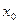 表示
表示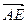 在
在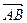 方向上的投影;
方向上的投影;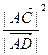 是否为定值?若是,求此定值,若不是,说明理由。
是否为定值?若是,求此定值,若不是,说明理由。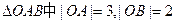 ,点P在线段AB的垂直平分线上,记向量
,点P在线段AB的垂直平分线上,记向量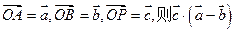 的值为 .
的值为 .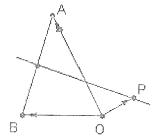
 与
与 满足
满足 ,且
,且 ,则△ABC为 ( )
,则△ABC为 ( )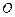 为△
为△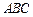 内一点,若任意
内一点,若任意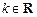 ,有
,有 ,则△
,则△