题目内容
2.在△ABC中,角A,B,C的对边分别为a,b,c,函数f(x)=(a+b+c)x2+2$\sqrt{ab}$x+a+b-c恰有一个零点,则角C的值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
分析 由题意知△=4ab-4(a+b+c)(a+b-c)=0,从而解得.
解答 解:∵函数f(x)=(a+b+c)x2+2$\sqrt{ab}$x+a+b-c恰有一个零点,
∴△=4ab-4(a+b+c)(a+b-c)=0,
即a2+b2-c2=-ab;
cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$,
故C=$\frac{2π}{3}$;
故选:D.
点评 本题考查了余弦定理的应用,属于基础题.

练习册系列答案
相关题目
14.下列几何体是台体的是( )
| A. | 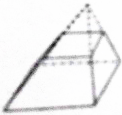 | B. | 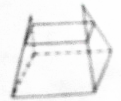 | C. |  | D. |  |
12.以椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左焦点为焦点的抛物线的标准方程是( )
| A. | y2=16x | B. | y2=-8x | C. | y2=-16x | D. | x2=-16y |
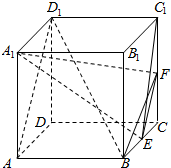 已知四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形且AA1⊥底面ABCD,AA1=4,E为BC的中点,F为CC1的中点.
已知四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形且AA1⊥底面ABCD,AA1=4,E为BC的中点,F为CC1的中点.