题目内容
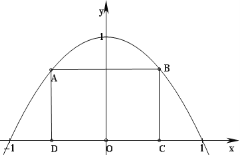
【题目】在直角坐标系![]() 中,过点
中,过点![]() 的直线与抛物线
的直线与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,弦
两点,弦![]() 的中点
的中点![]() 的轨迹记为
的轨迹记为![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(i)求![]() 的取值范围;
的取值范围;
(ii)![]() 轴上是否存在点
轴上是否存在点![]() ,使得当
,使得当![]() 变动时,总有
变动时,总有![]() ?说明理由.
?说明理由.
【答案】(1) ![]() ; (2) (i)
; (2) (i)![]() 或
或![]() .(ii)见解析.
.(ii)见解析.
【解析】
(1)先设![]() ,
,![]() ,
,![]() ,根据
,根据 ,以及题意,得到
,以及题意,得到![]() ,再由
,再由![]() ,两式联立,即可得出结果;
,两式联立,即可得出结果;
(2)(i)先由题意得到方程组![]() 有两不同实数解,消去
有两不同实数解,消去![]() ,根据判别式,以及题中条件,列出不等式求解,即可得出结果;
,根据判别式,以及题中条件,列出不等式求解,即可得出结果;
(ii)假设存在![]() 是符合题意的点;设
是符合题意的点;设![]() ,
,![]() ,联立直线与曲线方程,根据韦达定理,得到
,联立直线与曲线方程,根据韦达定理,得到![]() ,
,![]() ,计算
,计算![]() ,只需
,只需![]() ,即可得
,即可得![]() .
.
(1)设![]() ,
,![]() ,
,![]() ,由题意可得:
,由题意可得: ,
,
则![]() ,从而
,从而![]() ,
,
因为点![]() 为弦
为弦![]() 的中点,所以
的中点,所以![]() ,即
,即![]() ,
,
又直线![]() 过点
过点![]() ,所以
,所以![]() ,
,
则![]() ,即
,即![]() ,
,
而![]() 必在抛物线
必在抛物线![]() 的内部,从而
的内部,从而![]() ,即
,即![]() .
.
故![]() 的方程为
的方程为![]() .
.
(2)(i)因为直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,
所以方程组![]() 有两不同实数解,
有两不同实数解,
由![]() 消去
消去![]() ,得
,得![]() ,
,
即![]() 在
在![]() 上有两个不相等的实数根,
上有两个不相等的实数根,
所以,只需 且
且![]() ,
,
即 且
且![]() ,解得:
,解得:![]() 或
或![]() .
.
所以![]() 的取值范围是
的取值范围是![]() 或
或![]() ;
;
(ii)假设存在![]() 是符合题意的点;设
是符合题意的点;设![]() ,
,![]() .
.
将![]() 消去
消去![]() ,得
,得![]() ,故
,故![]() ,
,![]() ,
,
由(i)知:![]() 或
或![]() ;
;
从而
 ,
,
因此,当![]() ,即
,即![]() 时,
时,![]() ,
,
又![]() 为坐标原点,所以
为坐标原点,所以![]() ,
,
即存在点![]() 符合题意.
符合题意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目