题目内容
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() ,抛物线
,抛物线![]()
![]() 的焦点
的焦点![]() 是
是![]() 的一个顶点,设
的一个顶点,设![]() 是
是![]() 上的动点,且位于第一象限,记
上的动点,且位于第一象限,记![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.

(1)求![]() 的值和切线
的值和切线![]() 的方程(用
的方程(用![]() 表示)
表示)
(2)设![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与过
与过![]() 且垂直于
且垂直于![]() 轴的直线交于点
轴的直线交于点![]() .
.
(i)求证:点![]() 在定直线上;
在定直线上;
(ii)设![]() 与
与![]() 轴交于点
轴交于点![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ,切线
,切线![]() 方程为
方程为![]() (2)(ⅰ)证明见解析(ⅱ)
(2)(ⅰ)证明见解析(ⅱ)![]() 的最大值为
的最大值为![]()
【解析】
(1)根据椭圆的方程可求出过的定点,按照抛物线的标准方程即可求出![]() 的值;利用在点
的值;利用在点![]() 处的导数可求出直线的斜率,利用点斜式即可求出直线方程.(2)(i)利用点差法求出
处的导数可求出直线的斜率,利用点斜式即可求出直线方程.(2)(i)利用点差法求出![]() ,写出直线OD的方程,代入
,写出直线OD的方程,代入![]() ,可求出
,可求出![]() 为定值,即可证明. (ii)
为定值,即可证明. (ii)![]() 中,
中,![]() 为底,
为底,![]() 点的横坐标为高,用
点的横坐标为高,用![]() 表示三角形的面积,
表示三角形的面积,![]() 中,
中,![]() 为底,
为底,![]() 到
到![]() 的距离为高,依然用
的距离为高,依然用![]() 表示三角形的面积,换元求最值即可.
表示三角形的面积,换元求最值即可.
解:(I)由题意可得![]() ,
,![]() ,所以抛物线的焦点F为
,所以抛物线的焦点F为![]() ,则
,则![]() ,
,![]() .
.
直线![]() 的斜率为
的斜率为![]() ,所以切线方程
,所以切线方程![]() ,利用
,利用![]() 化简可得:
化简可得:![]() .
.
(2)(i)证明:设![]() ,
,![]()
由点差法可得![]() ,
,![]() ,即有
,即有![]() ,
,
直线OD的方程为![]() ,当
,当![]() 时,可得
时,可得![]() 即有点M在定直线
即有点M在定直线![]() 上;(ii)直线l的方程为
上;(ii)直线l的方程为![]() ,令
,令![]() ,可得
,可得![]() ,
,
则![]() ,
,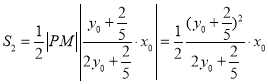
则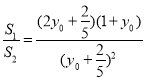 令
令![]() ,
,
则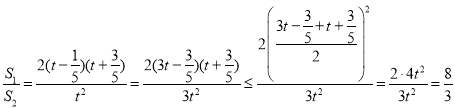
当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]()

【题目】某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
喜欢 | 不喜欢 | 合计 | |
大于40岁 | 20 | 5 | 25 |
20岁至40岁 | 10 | 20 | 30 |
合计 | 30 | 25 | 55 |
(1)判断是否有![]() 的把握认为喜欢“人文景观”景点与年龄有关?
的把握认为喜欢“人文景观”景点与年龄有关?
(2)已知20岁到40岁喜欢“人文景观”景点的市民中,有3位还比较喜欢“自然景观”景点,现在从20岁到40岁的10位市民中,选出3名,记选出喜欢“自然景观”景点的人数为![]() ,求
,求![]() 的分布列、数学期望.
的分布列、数学期望.
(参考公式:![]() ,其中
,其中![]() )
)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

