题目内容
过双曲线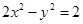
的右焦点作直线
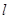交双曲线于
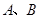两点，若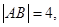
则这样的直线有
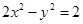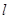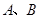的右焦点作直线交双曲线于两点，若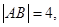则这样的直线有| A．4条 | B．3条 | C．2条 | D．1条 |
B
右焦点为（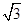
，0），当AB的斜率不存在时，直线AB方程为 x=，
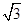代入双曲线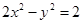
的方程可得y=±2，即A，B两点的纵坐标分别为2 和-2，满足|AB|=4．
当AB的斜率存在时，设直线AB方程为 y-0=k（x-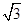），代入双曲线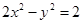的方程化简可得
（2-k2） x2-2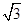 k2 x+3k2-2=0，∴x1+x2=
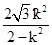，x1?x2=
，
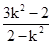∴|AB|=4=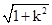
?
，平方化简可得 （3k4+6）（k2-1）=0，
∴k=±1，
所以，满足条件的且斜率存在的直线有2条．综上，所有满足条件的直线共有3条，
故答案为B．
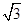，0），当AB的斜率不存在时，直线AB方程为 x=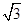，代入双曲线
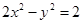的方程可得y=±2，即A，B两点的纵坐标分别为2 和-2，满足|AB|=4．当AB的斜率存在时，设直线AB方程为 y-0=k（x-
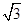），代入双曲线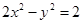的方程化简可得（2-k2） x2-2
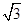k2 x+3k2-2=0，∴x1+x2=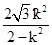，x1?x2=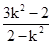，∴|AB|=4=
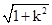?，平方化简可得 （3k4+6）（k2-1）=0，∴k=±1，
所以，满足条件的且斜率存在的直线有2条．综上，所有满足条件的直线共有3条，
故答案为B．
练习册系列答案
阅读快车系列答案
相关题目
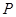是双曲线
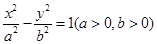与圆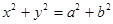
在第一象限的交点，其中
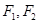分别是双曲线的左、右焦点，且
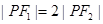，则双曲线的离心率为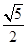
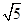
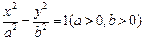的两条渐近线将平面划分为“上、下、左、右”四个区域（不含边界），若点
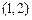在“上”区域内，则双曲线离心率
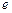的取值范围是 （ ）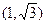
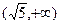
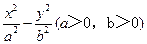的一条渐近线的斜率为
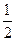，则该双曲线的离心率是 
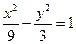有共同的渐近线，并且经过点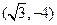
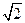且过点（4，－
）。
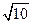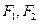为双
曲线C：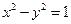
的左右焦点，点P在C上，
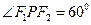，则P到x轴的距离为 
（ ）
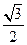
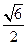
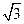
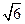
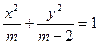表示双曲线，那么
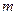的取值范围是 .
若直线
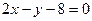沿向量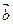
平移，所得直线过双曲线
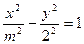的右焦点，
=" " （ii）双曲线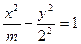
的离 心率e=" " ．
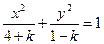表示双曲线，则
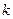的取值范围是 .