题目内容
【题目】已知数列{an}满足:a1=1,且当n2时,![]()
(1)若=1,证明数列{a2n1}是等差数列;
(2)若=2.①设![]() ,求数列{bn}的通项公式;②设
,求数列{bn}的通项公式;②设![]() ,证明:对于任意的p,m N *,当p m,都有
,证明:对于任意的p,m N *,当p m,都有![]() Cm.
Cm.
【答案】(1)证明见解析;(2)①![]() ;②证明见解析
;②证明见解析
【解析】
(1)分别可得![]() ,
,![]() ,二者求和可得
,二者求和可得![]() ,进而得证;
,进而得证;
(2)①分别可得![]() ,
,![]() ,二者整理可得
,二者整理可得![]() ,即可证明
,即可证明![]() 是首项为
是首项为![]() ,公比为4的等比数列,进而求得通项公式;
,公比为4的等比数列,进而求得通项公式;
②先求得![]() 与
与![]() 的通项公式,则
的通项公式,则![]()
![]() ,则
,则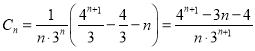 ,进而利用数列的单调性证明即可
,进而利用数列的单调性证明即可
(1)证明:当![]() 时,
时,![]() ,
,
![]() ①,
①,
![]() ②,
②,
则①![]() ②得
②得![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列
(2)①当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ①,
①,
![]() ②,
②,
①![]() ②
②![]() 得
得![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() 是首项为
是首项为![]() ,公比为4的等比数列,
,公比为4的等比数列,
![]()
②由(2)①知![]() ,
,
同理由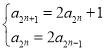 可得
可得![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 是首项为
是首项为![]() ,公比为4的等比数列,
,公比为4的等比数列,
![]() ,
,
![]()
![]()
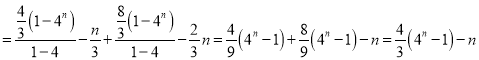 ,
,
 ,
,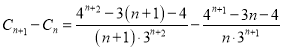
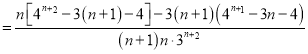
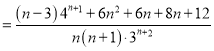
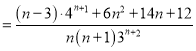
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
![]() 对于一切
对于一切![]() ,都有
,都有![]() ,故对任意
,故对任意![]() ,当
,当![]() 时,
时,![]()

练习册系列答案
相关题目