题目内容
【题目】在平面直角坐标系![]() 中取两个定点
中取两个定点![]() ,
,![]() ,再取两个动点
,再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(1)求直线![]() 与
与![]() 的交点
的交点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴且与轨迹
轴且与轨迹![]() 交于另一点
交于另一点![]() ,
,![]() 为轨迹
为轨迹![]() 的右焦点,若
的右焦点,若![]() ,求证:
,求证:![]()
【答案】(1)![]() ; (2)证明见解析
; (2)证明见解析
【解析】
(1)由直线所过两点可得直线![]() 和
和![]() 的方程,设
的方程,设![]() 为两直线交点,则两方程做乘法整理可得所求轨迹方程;
为两直线交点,则两方程做乘法整理可得所求轨迹方程;
(2)设过![]() 直线
直线![]() 及
及![]() 坐标,将直线方程与椭圆方程联立整理可得韦达定理的形式;由
坐标,将直线方程与椭圆方程联立整理可得韦达定理的形式;由![]() 可得
可得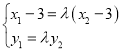 ;通过分析法可知,若要证
;通过分析法可知,若要证![]() ,只需证得
,只需证得![]() ,将等式整理后可知最终只需证得
,将等式整理后可知最终只需证得![]() ,将韦达定理的结论代入即可知等式成立,即所证
,将韦达定理的结论代入即可知等式成立,即所证![]() 成立.
成立.
(1)由题意知,直线![]() 的方程为:
的方程为:![]() …①
…①
直线![]() 的方程为:
的方程为:![]() …②
…②
设![]() 是直线
是直线![]() 与
与![]() 的交点,
的交点,
①×②得:![]() ,整理得:
,整理得:![]()
即点![]() 的轨迹
的轨迹![]() 的方程为:
的方程为:![]()
(2)证明:设过点![]() 的直线
的直线![]() ,
,![]() ,
,![]() ,则
,则![]()
由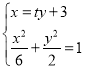 消去
消去![]() 得:
得:![]()
![]() ,
,![]()
由![]() 得:
得: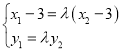
由(1)知:![]() ,则要证
,则要证![]() ,即证
,即证![]()
只需证![]() ,只需
,只需![]()
即证![]()
又![]() ,
,![]()
![]() ,即
,即![]()
![]() 成立
成立 ![]() 成立
成立

 优质课堂快乐成长系列答案
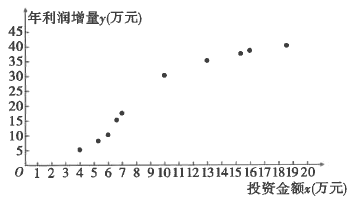
优质课堂快乐成长系列答案【题目】某果园种植“糖心苹果”已有十余年,为了提高利润,该果园每年投入一定的资金,对种植采摘包装宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额![]() (单位:万元)与年利润增量
(单位:万元)与年利润增量![]() (单位:万元)的散点图:
(单位:万元)的散点图:
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了![]() 关于
关于![]() 的两个回归模型;
的两个回归模型;
模型①:由最小二乘公式可求得![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() ;
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:![]() 的附近,对投资金额
的附近,对投资金额![]() 做交换,令
做交换,令![]() ,则
,则![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)分别利用这两个回归模型,预测投资金额为20万元时的年利润增量(结果保留两位小数);
(3)根据下列表格中的数据,比较两种模型的相关指数![]() ,并说明谁的预测值精度更高更可靠.
,并说明谁的预测值精度更高更可靠.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:样本![]() 的最小乘估计公式为
的最小乘估计公式为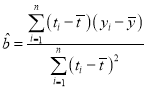 ,
,![]() ;
;
相关指数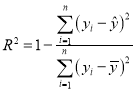 .
.
参考数据:![]() ,
,![]() .
.
【题目】某果园种植“糖心苹果”已有十余年,根据其种植规模与以往的种植经验,产自该果园的单个“糖心苹果”的果径(最大横切面直径,单位:![]() )在正常环境下服从正态分布
)在正常环境下服从正态分布![]() .
.
(1)一顾客购买了20个该果园的“糖心苹果”,求会买到果径小于56![]() 的概率;
的概率;
(2)为了提高利润,该果园每年投入一定的资金,对种植、采摘、包装、宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额![]() (单位:万元)与年利润增量
(单位:万元)与年利润增量![]() (单位:万元)的散点图:
(单位:万元)的散点图:
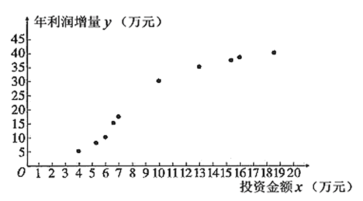
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了![]() 关于
关于![]() 的两个回归模型;
的两个回归模型;
模型①:由最小二乘公式可求得![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() ;
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:![]() 的附近,对投资金额
的附近,对投资金额![]() 做交换,令
做交换,令![]() ,则
,则![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测投资金额为20万元时的年利润增量(结果保留两位小数).
,并选择拟合精度更高、更可靠的模型,预测投资金额为20万元时的年利润增量(结果保留两位小数).
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:若随机变量![]() ,则
,则![]() ,
,![]() ;样本
;样本![]() 的最小乘估计公式为
的最小乘估计公式为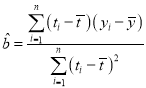 ,
,![]() ;
;
相关指数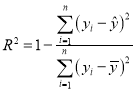 .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.