题目内容
【题目】在平面直角坐标系
中，直线
的参数方程为
（
为参数），直线
的参数方程为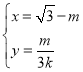
（
为参数），设直线与的交点为
，当
变化时点的轨迹为曲线
.
（1）求出曲线的普通方程；
（2）以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，直线
的极坐标方程为
，点
为曲线上的动点，求点到直线的距离的最大值.
【答案】（1）
；（2）
.
【解析】
（1）直接利用转换关系的应用，把参数方程极和直角坐标方程之间进行转换．
（2）利用点到之间的距离公式的应用和三角函数关系式的变换及正弦型函数的性质的应用求出结果．
解：（1）将
，
的参数方程转化为普通方程.
：
，
：
，
两式相乘消
可得
，
因为
，所以
，所以
的普通方程为.
（2）直线
的直角坐标方程为
，
由（1）知曲线与直线无公共点.
由于的参数方程为
（
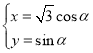为参数，
，
），
所以曲线上的点
到直线的距离为
，
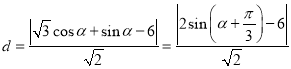所以当
时，
的最大值为.
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】某市劳动部门坚持就业优先，釆取多项措施加快发展新兴产业，服务经济，带来大量就业岗位，据政府工作报告显示，截至2018年末，全市城镇新增就业21.9万人，创历史新高．城镇登记失业率为4.2%，比上年度下降0.73个百分点，处于近20年来的最低水平．
（1）现从该城镇适龄人群中抽取100人，得到如下列联表：
失业 | 就业 | 合计 | |
男 | 3 | 62 | 65 |
女 | 2 | 33 | 35 |
合计 | 5 | 95 | 100 |
根据联表判断是否有99%的把握认为失业与性别有关？
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（2）调查显示，新增就业人群中，新兴业态，民营经济，大型国企对就业支撑作用不断增强，其岗位比例为2∶5∶3，现要抽取一个样本容量为50的样本，则这三种岗位应该各抽取多少人？
