题目内容
15．设集合A到B的映射为f1：x→y=2x+1，集合B到C的映射为f2：y→z=y2-1，则集合A到C的映射f的对应法则是什么？集合A中的元素1在C中的象是什么？集合C中的元素0在A中的原象又是什么？分析 根据集合A到B的映射为f1：x→y=2x+1，集合B到C的映射为f2：y→z=y2-1，可得集合A到C的映射f的对应法则；令x=1，可得集合A中的元素1在C中的象；令4x2+4x=0，可得集合C中的元素0在A中的原象．
解答 解：∵集合A到B的映射为f1：x→y=2x+1，集合B到C的映射为f2：y→z=y2-1，
则集合A到C的映射f的对应法则是z=（2x+1）2-1=4x2+4x，
则集合A中的元素1在C中的象是8，
令4x2+4x=0，则x=0，或x=-1，
即集合C中的元素0在A中的原象是0，或-1
点评 本题考查的知识点是映射的定义，熟练掌握并正确理解映射的定义，是解答的关键．
练习册系列答案
相关题目
10．1+4+7+10+…+（3n+4）+（3n+7）等于（ ）
| A． | $\frac{n（3n+8）}{2}$ | B． | $\frac{（n+2）（3n+8）}{2}$ | C． | $\frac{（n+3）（3n+8）}{2}$ | D． | $\frac{n（3n-1）}{2}$ |
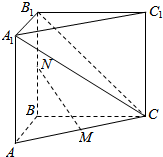如图在三棱柱ABC-A1B1C1中，AB=BC=2，AC=2$\sqrt{2}$，侧面ABB1A1是矩形，M，N分别是AC，BB1的中点．