题目内容
17.已知 A={x|x=4n+1,n∈Z},B={x|x=8n+1,n∈Z},判断A、B之间的关系是A?B(用⊆或?或∈或∉填空)分析 将“x=8n+1,n∈Z”变为“x=4•2n+1,n∈Z”,由集合的包含关系即可得到A、B之间的关系.
解答 解:∵B={x|x=8n+1,n∈Z}={x|x=4•2n+1,n∈Z},且A={x|x=4n+1,n∈Z},
2n是偶数,n是整数,
∴A?B,
故答案为:?.
点评 本题考查集合之间的包含关系,属于基础题.

练习册系列答案
相关题目
7.直线l:y=kx+1与圆x2+y2=1相交于A,B两点,则“△OAB的面积为$\frac{{\sqrt{3}}}{4}$”是“k=$\sqrt{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.因为正切函数是奇函数,f(x)=tan(x2+1)是正切函数,所以f(x)=tan(x2+1)是奇函数,以上推理( )
| A. | 结论正确 | B. | 大前提不正确 | C. | 小前提不正确 | D. | 全不正确 |
7. 正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
 正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )| A. | 20152 | B. | 20162 | C. | 2015+2016 | D. | 2015×2016 |
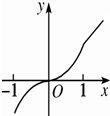
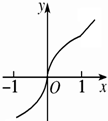
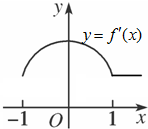 已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )
已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )