题目内容
利民商店经销某种洗衣粉,年销售量为6000包,每包进价2.80元,销售价3.40元,全年分若干次进货,每次进货x包,已知每次进货运输劳务费62.50元,全年保管费为1.5x元。
(1)把该商店经销洗衣粉一年的利润y(元)表示为每次进货量x(包)的函数,并指出函数的定义域;
(2)为了使利润最大,每次应该进货多少包?
(1)把该商店经销洗衣粉一年的利润y(元)表示为每次进货量x(包)的函数,并指出函数的定义域;
(2)为了使利润最大,每次应该进货多少包?
(1)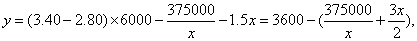
函数的定义域是 (2)500
(2)500
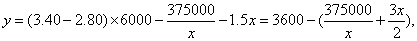
函数的定义域是
 (2)500
(2)500试题分析:(1)若每次进洗衣粉x包,则全年共需进洗衣粉
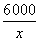 次,
次,而全年所需运输劳务费是
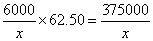 元,而全年保管费为1.5x元,
元,而全年保管费为1.5x元,所以全年的总利润为
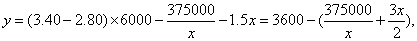
函数的定义域是

(2)
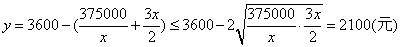
当且仅当
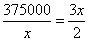 ,即当
,即当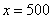 时,上式中等号成立,
时,上式中等号成立,此时y的最大值为2100元,即为了获得最大利润2100元,每次应进洗衣粉500包。
点评:利用函数知识解数学应用问题的一般步骤是:①审题:弄清题意,分清条件和结论,理顺数量关系;②建模:将文字语言转化成数学语言,利用函数及有关数学知识,建立相应的数学模型;③求模:求解数学模型;利用数学的方法及函数的知识去解得到的数学模型,求解数学结果.④还原:将数学方法得到的结论还原为实际问题的结论,使实际问题得以解决.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
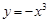
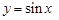
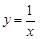
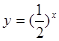
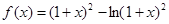 ,若关于
,若关于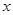 的方程
的方程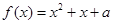 在
在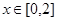 上恰好有两个相异实根,则实数
上恰好有两个相异实根,则实数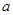 的取值范围为______________.
的取值范围为______________.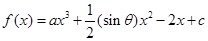 的图象过点
的图象过点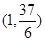 ,且在
,且在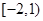 内单调递减,在
内单调递减,在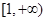 上单调递增。
上单调递增。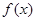 的解析式;
的解析式;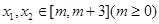 ,不等式
,不等式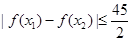 恒成立,试问这样的
恒成立,试问这样的 是否存在.若存在,请求出
是否存在.若存在,请求出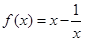 ,对任意
,对任意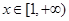 ,
,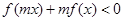 恒成立,则实数
恒成立,则实数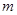 的取值范围是______________.
的取值范围是______________.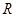 上的函数
上的函数 是最小正周期为
是最小正周期为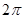 的偶函数,当
的偶函数,当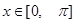 时,
时,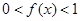 ,且在
,且在 上单调递减,在
上单调递减,在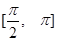 上单调递增,则函数
上单调递增,则函数 在
在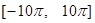 上的零点个数为 .
上的零点个数为 .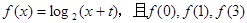 成等差数列,点
成等差数列,点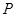 是函数
是函数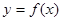 图像上任意一点,点
图像上任意一点,点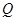 的轨迹是函数
的轨迹是函数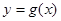 的图像。
的图像。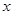 的不等式
的不等式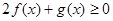 ;
;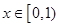 时,总有
时,总有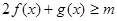 恒成立,求
恒成立,求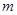 的取值范围。
的取值范围。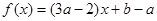 ,
, 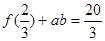 ,且
,且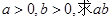 的取值范围
的取值范围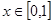 时,
时,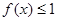 恒成立,且
恒成立,且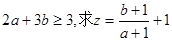 的取值范围
的取值范围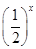
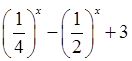 的值域 .
的值域 .