已知函数f(x)=$\left\{\begin{array}{l}{lgx.x≥\frac{3}{2}}\\{lg(3-x).x＜\frac{3}{2}}\end{array}\right.$.若方程f(x)=k无实数根.则实数k的取值范围是k＜$lg\frac{3}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

16．已知函数f（x）=$\left\{\begin{array}{l}{lgx，x≥\frac{3}{2}}\\{lg（3-x），x＜\frac{3}{2}}\end{array}\right.$，若方程f（x）=k无实数根，则实数k的取值范围是k＜$lg\frac{3}{2}$．

分析若方程f（x）=k无实数根，则函数f（x）的图象与直线y=k无交点，数形结合分析函数的值域，可得答案．

解答解：方程f（x）=k无实数根，则函数f（x）的图象与直线y=k无交点，
函数f（x）=$\left\{\begin{array}{l}{lgx，x≥\frac{3}{2}}\\{lg（3-x），x＜\frac{3}{2}}\end{array}\right.$的图象如下图所示：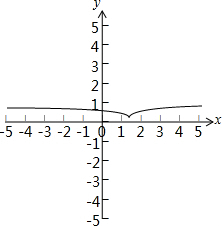

由图可得：函数f（x）的值域为[$lg\frac{3}{2}$，+∞）
则k＜$lg\frac{3}{2}$，
故答案为：k＜$lg\frac{3}{2}$

点评本题考查的知识点是函数零点与方程的根，数形结合思想，难度中档．

练习册系列答案

千里马走向假期期末仿真试卷寒假系列答案

新锐图书假期园地暑假作业中原农民出版社系列答案

相关题目

6．几何体的三视图和相关数据如图所示，则该几何体的体积为（　　）

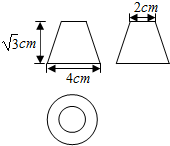
A．

$\frac{{7\sqrt{3}π}}{3}$

B．

$\frac{{8\sqrt{3}π}}{3}$

7．函数y=$\sqrt{sinx}$+$\sqrt{-tanx}$有意义．则x的取值范围是（2k$π+\frac{π}{2}$，2kπ+π]，k∈Z．

4．函数f（x²-3）=log₂$\frac{{x}^{2}+6}{{x}^{2}+1}$，函数g（x）是定义在R上的奇函数，当x＞0时，g（x）=2^x．
（1）求f（x）和g（x）的解析式；
（2）求关于x的方程g（x）=f（1）+a在实数集R内有解，求实数a的取值范围．

11．已知$\frac{sinθ+cosθ}{sinθ-cosθ}$=2，则sinθcosθ的值是（　　）

1．已知点（p，q）是平面直角坐标系xOy上一点，x₁，x₂是方程x²-px+q=0的两个实根．记φ（p，q）=max{|x₁|，|x₂|}（表示|x₁|，|x₂|中的最大值）．过点A（2，1）作抛物线L：y=$\frac{1}{4}$x²的切线交y轴于点B，对线段AB上的任一点Q（p，q），求φ（p，q）的值．

8．已知函数f（x）=$\left\{\begin{array}{l}{{3}^{x}\\;（x≥0）}\\{lo{g}_{3}（-x）\\;（x＜0）}\end{array}\right.$．若函数g（x）=f²（x）+f（x）+t，（t∈R），则下列说法中不正确的是（　　）

	A．	当t＜-2时，则函数g（x）有四个零点		B．	当t=-2时，则函数g（x）有三个零点
	C．	当t=$\frac{1}{4}$时，则函数g（x）有一个零点		D．	当-2＜t＜$\frac{1}{4}$时，则函数g（x）有两个零点

5．已知集合A={y|y=e^x（x∈R⁺}，B={y|y＞a}，若A⊆B，则实数a的取值范围是（-∞，1]．

14．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上存在一点P满足|OP|为边长的正方形的面积等于2ab（其中O为坐标原点），则双曲线的离心率的取值范围是（　　）

A．

（1，$\frac{\sqrt{5}}{2}$]

B．

（1，$\frac{\sqrt{7}}{2}$]

C．

[$\frac{\sqrt{5}}{2}$，+∞）

D．

[$\frac{\sqrt{7}}{2}$，+∞）

试题分类