题目内容
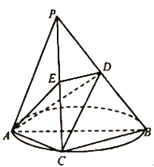
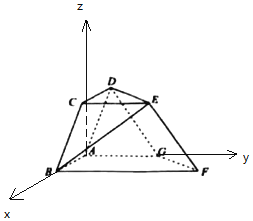
【题目】在如图所示的几何体中,侧面ABCD为矩形,侧面DEFG为平行四边形,AB=1,AD=2,AG∥BF,AB⊥BF,AG=3,BF=5,二面角D﹣AB﹣F的大小为60°.
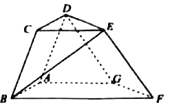
(1)证明,平面CDE⊥平面ADG
(2)求直线BE与平面ABCD所成角的大小
【答案】(1)见解析;(2)30°
【解析】
(1)根据AB⊥BF,进而证明CD⊥平面ADG,即可.
(2)由题可以A为原点,AB,AG所在直线分别为x,y轴,建立空间直角坐标系,根据二面角
D﹣AB﹣F的大小为60°可得∠DAG=60°,再根据边角关系与空间向量的方法求解直线BE与平面ABCD所成角的大小即可.
(1)由AB⊥BF,CD∥AB,AG∥BF,得CD⊥AG,又CD⊥AD,∴CD⊥平面ADG,
平面CDE⊥平面ADG.
(2)以A为原点,AB,AG所在直线分别为x,y轴,建立空间直角坐标系,
∵AB⊥AD,AB⊥AG,∴∠DAG是二面角D﹣AB﹣F的平面角,∴∠DAG=60°,
∴D(0,1,![]() ),B(1,0,0),G(0,3,0),F(1,5,0),
),B(1,0,0),G(0,3,0),F(1,5,0),
由![]() =
=![]() ,得E(1,3,
,得E(1,3,![]() ),设平面ABCD的法向量
),设平面ABCD的法向量![]() =(x,y,z),
=(x,y,z),
则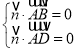 ,∴
,∴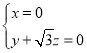 ,令z=﹣1,得
,令z=﹣1,得![]() =(0,
=(0,![]() ),
),
设BE与平面ABCD所成角为θ,则sinθ=![]() =
=![]() ,解得θ=30°.
,解得θ=30°.
故直线BE与平面ABCD所成角的大小为30°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
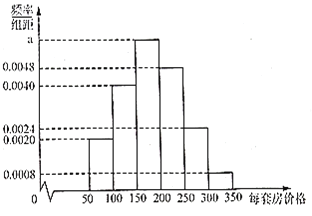
小学生10分钟应用题系列答案【题目】某房产销售公司从登记购房的客户中随机选取了50名客户进行调查,按他们购一套房的价格(万元)分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 得到频率分布直方图如图所示.用频率估计概率.
得到频率分布直方图如图所示.用频率估计概率.
房产销售公司每卖出一套房,房地产商给销售公司的佣金如下表(单位:万元):
房价区间 |
|
|
|
|
|
|
佣金收入 | 1 | 2 | 3 | 4 | 5 | 6 |
(1)求![]() 的值;
的值;
(2)求房产销售公司卖出一套房的平均佣金;
(3)若该销售公司平均每天销售4套房,请估计公司月(按30天计)利润(利润=总佣金-销售成本).
该房产销售公司每月(按30天计)的销售成本占总佣金的百分比按下表分段累计/span>计算:
月总佣金 | 不超过100万元的部分 | 超过100万元至200万元的部分 | 超过200万元至300万元的部分 | 超过300万元的部分 |
销售成本占 佣金比例 |
|
|
|
|
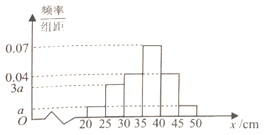
【题目】某农科站技术员为了解某品种树苗的生长情况,在该批树苗中随机抽取一个容量为100的样本,测量树苗高度(单位:![]() ).经统计,高度在区间
).经统计,高度在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图,其中高度不低于
分成6组,制成如图所示的频率分布直方图,其中高度不低于![]() 的树苗为优质树苗.
的树苗为优质树苗.
附:
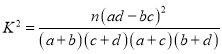 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
(1)求频率分布直方图中![]() 的值;
的值;
(2)已知所抽取的这100棵树苗来自于甲、乙两个地区,部分数据如下![]() 列联表所示,将列联表补充完整,并根据列联表判断是否有
列联表所示,将列联表补充完整,并根据列联表判断是否有![]() %的把握认为优质树苗与地区有关?
%的把握认为优质树苗与地区有关?
甲地区 | 乙地区 | 合计 | |
优质树苗 | 5 | ||
非优质树苗 | 25 | ||
合计 |
【题目】汽车是碳排放量比较大的行业之一,欧盟规定,从2015年开始,将对![]() 排放量超过130g/km的
排放量超过130g/km的![]() 型新车进行惩罚(视为排放量超标),某检测单位对甲、乙两类
型新车进行惩罚(视为排放量超标),某检测单位对甲、乙两类![]() 型品牌抽取5辆进行
型品牌抽取5辆进行![]() 排放量检测,记录如下(单位:g/km):
排放量检测,记录如下(单位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | y | 160 |
经测算发现,乙品牌车![]() 排放量的平均值为
排放量的平均值为![]() .
.
(Ⅰ)从被检测的5辆甲类品牌中任取2辆,则至少有一辆![]() 排放量超标的概率是多少?
排放量超标的概率是多少?
(Ⅱ)若乙类品牌的车比甲类品牌的![]() 的排放量的稳定性要好,求x的范围.
的排放量的稳定性要好,求x的范围.