��Ŀ����
����Ŀ��һ�����С��Ϸ�Ĺ������£�ÿ����Ϸ����������Σ�ÿ�λ��ĺ�Ҫô����һ�����֣�Ҫô���������֣�ÿ����Ϸ�������κ����������ֻ��150�֣������������ֻ��100�֣�����һ�����ֻ��50�֣�û�г�����������-300��.��ÿ�λ��ij������ֵĸ���Ϊ![]() ���Ҹ��λ��ij������������.
���Ҹ��λ��ij������������.
��1����һ����Ϸ�н�����һ�����ֵĸ���Ϊ![]() ����
����![]() �����ֵ��
�����ֵ��![]() ��
��
��2���ԣ�1����ȷ����![]() ��Ϊ
��Ϊ![]() ��ֵ����3����Ϸ���������ֵ�����Ϊ�������
��ֵ����3����Ϸ���������ֵ�����Ϊ�������![]() ����ÿ����Ϸ�������ֵĸ���
����ÿ����Ϸ�������ֵĸ���![]() �����������
�����������![]() ������
������![]() ��
��
��3����������Ϸ�������˶����֣���������Ϸ��������ķ�����ȣ�����û�����ӷ���������.�����ø���ͳ�Ƶ����֪ʶ�����������ٵ�ԭ��.
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3��������.
����3��������.
��������
��1�����ݶ����ظ������и��ʼ���,�ɵý�����һ�����ֵĸ���![]() .Ȼ����õ�����
.Ȼ����õ�����![]() ,����
,����![]() ��ü�ֵ��.�ٸ���
��ü�ֵ��.�ٸ���![]() �ĵ������,���
�ĵ������,���![]() �����ֵ.
�����ֵ.
��2���ɣ�1����֪,![]() .����ò��������ֵĸ���, �ɶ����¼��������ʼ�����ó������ֵĸ���.��϶���ֲ���������,���ɵ��������
.����ò��������ֵĸ���, �ɶ����¼��������ʼ�����ó������ֵĸ���.��϶���ֲ���������,���ɵ��������![]() ������
������![]() ;
;
��3�����ÿ���÷ֵĸ���,���ݹ�ʽ������õ÷ֵ���ѧ����.���캯��,���õ���������֤����ѧ����Ϊ����,����˵����������.
��1�������֪,һ����Ϸ�н�����һ�����ֵĸ���Ϊ��
![]() ,
,
![]()
��![]() ��
��![]() ��
��![]() ���ᣩ
���ᣩ
��![]() ʱ,
ʱ,![]() ��
��
��![]() ʱ,
ʱ,![]() ,
,
��![]() ��
��![]() �ϵ�������,��
�ϵ�������,��![]() �ϵ����ݼ�,
�ϵ����ݼ�,
�൱![]() ʱ,
ʱ,![]() �����ֵ,��
�����ֵ,��![]() �����ֵ��
�����ֵ��![]() ��
��
��2���ɣ�1����֪,![]()
��ÿ����Ϸ�������ֵĸ���Ϊ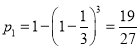
�����֪![]()
��![]() ��
��
��3���������ÿ����Ϸ�ĵ÷�Ϊ�������![]() ,��
,��![]() �Ŀ���ֵΪ-300,50,100,150��
�Ŀ���ֵΪ-300,50,100,150��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]()
![]() ��
��
��![]() ,��
,��![]() ��
��
����![]() ��
��![]() ����������
����������
��![]() ��
��
����![]() ��
��
��˵��ÿ����Ϸƽ���÷��Ǹ���,�ɸ���ͳ�Ƶ����֪ʶ��֪��������������Ϸ��,������ķ������,����û�����ӷ��������.

����Ŀ��ijУ��һ�β����и����꼶ѧ������ѧ�ɼ�ͳ�����±���ʾ���ڲμӲ��Ե�ѧ������ȡ1�ˣ���ɼ�������120�ֵĸ���Ϊ![]() .
.
���� |
|
|
|
|
|
|
|
Ƶ�� | 40 | 50 | 70 | 60 | 80 |
| 50 |
��1����![]() ��ֵ��
��ֵ��
��2�������շֲ�����ķ����ӳɼ���![]() ��
��![]() ��ѧ���г�ȡ6�ˣ��ٴ���6���������ȡ2�˽��д������������2����������1�˵ķ�����
��ѧ���г�ȡ6�ˣ��ٴ���6���������ȡ2�˽��д������������2����������1�˵ķ�����![]() �ĸ���.
�ĸ���.