题目内容
记函数f(x)=
(a≠0).
(1)试求函数f(x)的定义域和值域;
(2)当a=b=1时,函数f(x)的图象能否由函数y=
的图象变换得到?若能,则写出变换过程,并作出函数图象;若不能,则说明理由.
| bx+2 |
| ax+1 |
(1)试求函数f(x)的定义域和值域;
(2)当a=b=1时,函数f(x)的图象能否由函数y=
| 1 |
| x |
(1)由ax+1≠0得f(x)的定义域为{x|x≠-
},(2分)
f(x)=
=
=
+
,(4分)
∵
≠0,∴函数f(x)的值域为{y|y≠
};(6分)
(2)当a=b=1时,函数f(x)=1+
(7分)
由函数y=
的图象向左平移1个单位,得到函数y=
的图象(9分)
再由函数y=
的图象向上平移1个单位,得到函数f(x)=1+
的图象(11分)
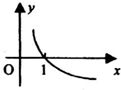
故,函数f(x)=1+
的图象为:
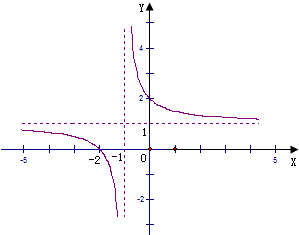
| 1 |
| a |
f(x)=
| bx+2 |
| ax+1 |
| ||||
| ax+1 |
| b |
| a |
2-
| ||
| ax+1 |
∵
2-
| ||
| ax+1 |
| b |
| a |
(2)当a=b=1时,函数f(x)=1+
| 1 |
| x+1 |
由函数y=
| 1 |
| x |
| 1 |
| x+1 |
再由函数y=
| 1 |
| x+1 |
| 1 |
| x+1 |
故,函数f(x)=1+
| 1 |
| x+1 |


练习册系列答案
相关题目
 .
. 上画出函数
上画出函数 的图像;
的图像;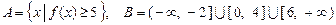 . 试判断集合
. 试判断集合 和
和 之间的关系,并给出证明;
之间的关系,并给出证明; 时,求证:在区间
时,求证:在区间 上,
上, 的图像位于函数
的图像位于函数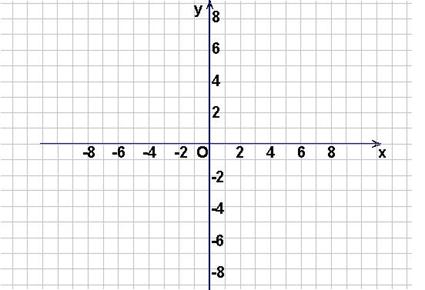
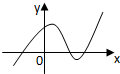
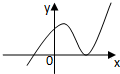
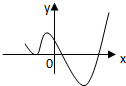
 的反函数是( )
的反函数是( )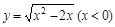







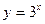 与
与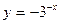 的图象关于下列那种图形对称( )
的图象关于下列那种图形对称( ) 轴
轴 轴
轴
 ,则
,则 .
.