题目内容
已知f(x)=ax3+bx2+cx+d(a≠0),记△=4(b2-3ac),则当△≤0且a>0时,f(x)的大致图象为( )
A. | B.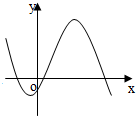 | C. | D. |
∵f(x)=ax3+bx2+cx+d(a≠0),
∴f′(x)=3ax2+2bx+c
∵△=4(b2-3ac)≤0
又∵a>0
∴f′(x)≥0恒成立
故f(x)=ax3+bx2+cx+d在R上为增函数,
故选C
∴f′(x)=3ax2+2bx+c
∵△=4(b2-3ac)≤0
又∵a>0
∴f′(x)≥0恒成立
故f(x)=ax3+bx2+cx+d在R上为增函数,
故选C

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 ,则其反函数
,则其反函数 的图像是 ( )
的图像是 ( )
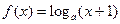 ,点
,点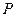 是函数
是函数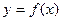 图像上任意一点,点
图像上任意一点,点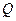 的轨迹是函数
的轨迹是函数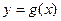 的图像. (Ⅰ)当
的图像. (Ⅰ)当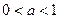 时,解关于
时,解关于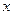 的不等式
的不等式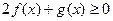 ; (Ⅱ)当
; (Ⅱ)当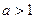 ,且
,且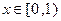 时,总有
时,总有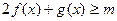 恒成立,求
恒成立,求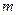 的取值范围.
的取值范围.
 的图象大致是( )
的图象大致是( )
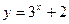 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象则
的图象则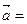
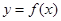 是函数
是函数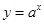 (
(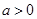 ,且
,且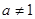 )的反函数,其图象经过点
)的反函数,其图象经过点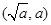 ,则
,则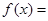 ( )
( )


