题目内容
已知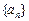 是首项为2,公比为
是首项为2,公比为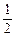 的等比数列,
的等比数列,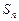 为它的前
为它的前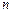 项和.
项和.
(1)用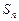 表示
表示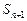 ;
;
(2)是否存在自然数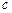 和
和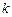 ,使得
,使得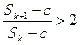 成立.
成立.
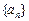 是首项为2,公比为
是首项为2,公比为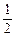 的等比数列,
的等比数列,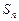 为它的前
为它的前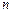 项和.
项和.(1)用
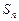 表示
表示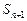 ;
;(2)是否存在自然数
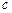 和
和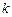 ,使得
,使得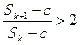 成立.
成立.(1)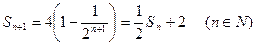
(2)不存在自然数c、k,使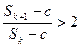 成立
成立
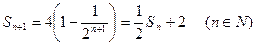
(2)不存在自然数c、k,使
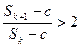 成立
成立(1)由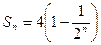 ,得
,得
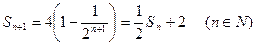

(2)要使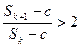 ,只要
,只要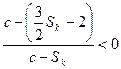

因为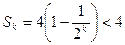 ,所以
,所以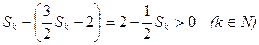 ,故只要
,故只要
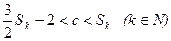
 ①
①
因为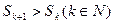 ,所以
,所以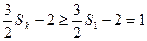 ,
,
又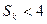 ,故要使①成立,c只能取2或3
,故要使①成立,c只能取2或3
当c=2时,因为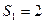 ,所以当k=1时,
,所以当k=1时,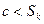 不成立,从而①不成立
不成立,从而①不成立
因为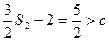 ,由
,由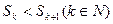 ,得
,得
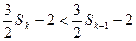 ,所以当
,所以当 时,
时,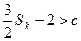 ,从而①不成立
,从而①不成立
当c=3时,因为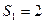 ,
,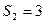 ,
,
所以当k=1,2时,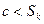 不成立,从而①不成立
不成立,从而①不成立
因为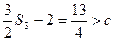 ,又
,又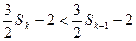 ,
,
所以当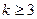 时,
时,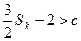 ,从而①不成立
,从而①不成立
故不存在自然数c、k,使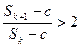 成立
成立
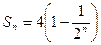 ,得
,得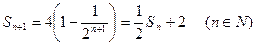

(2)要使
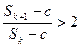 ,只要
,只要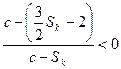

因为
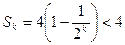 ,所以
,所以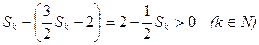 ,故只要
,故只要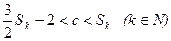
 ①
①因为
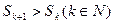 ,所以
,所以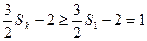 ,
,又
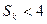 ,故要使①成立,c只能取2或3
,故要使①成立,c只能取2或3
当c=2时,因为
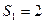 ,所以当k=1时,
,所以当k=1时,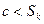 不成立,从而①不成立
不成立,从而①不成立
因为
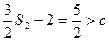 ,由
,由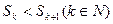 ,得
,得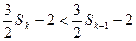 ,所以当
,所以当 时,
时,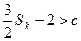 ,从而①不成立
,从而①不成立
当c=3时,因为
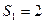 ,
,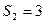 ,
,所以当k=1,2时,
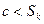 不成立,从而①不成立
不成立,从而①不成立
因为
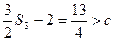 ,又
,又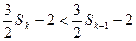 ,
,所以当
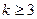 时,
时,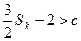 ,从而①不成立
,从而①不成立
故不存在自然数c、k,使
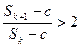 成立
成立

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
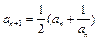 ,{bn}中
,{bn}中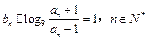 .
.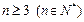 时,证明:
时,证明: .
.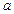 元,每期利率为
元,每期利率为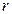 ,设本利和为
,设本利和为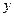 ,存期为
,存期为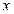 ,写出本利和
,写出本利和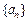 的前n项和
的前n项和 满足
满足 ,
, 为等比数列,且
为等比数列,且 ,
, ,
, ,
, ;
; ,求数列
,求数列 的前n项和
的前n项和 .
.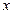 的多项式
的多项式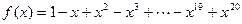 表为关于
表为关于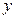 的多项式
的多项式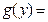
 其中
其中 则
则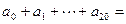 .
. 为等比数列
为等比数列 的前
的前 项和,
项和, ,则
,则
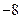

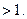 y
y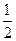 bx.
bx. 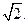
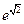
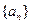 满足:
满足: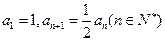 ,
,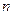 项和为
项和为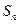 ,则
,则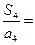 .
.