ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥΤ’ΦΑΜΖ±Θ÷Σ ΕΘ§‘ω«Ω―ß…ζΒΡΜΖ±Θ“β ΕΘ§‘Ύ»Ϊ–ΘΉι÷·ΝΥ“Μ¥Έ”–ΙΊΜΖ±Θ÷Σ ΕΒΡΨΚ»ϋΘ§Ψ≠Ιΐ≥θ»ϋΓΔΗ¥»ϋΘ§ΦΉΓΔ““ΝΫΗω¥ζ±μΕ”Θ®ΟΩΕ”![]() »ΥΘ©Ϋχ»κΝΥΨω»ϋΘ§ΙφΕ®ΟΩ»ΥΜΊ¥π“ΜΗωΈ ΧβΘ§¥πΕ‘ΈΣ±ΨΕ””°ΒΟ
»ΥΘ©Ϋχ»κΝΥΨω»ϋΘ§ΙφΕ®ΟΩ»ΥΜΊ¥π“ΜΗωΈ ΧβΘ§¥πΕ‘ΈΣ±ΨΕ””°ΒΟ![]() Ζ÷Θ§¥π¥μΒΟ
Ζ÷Θ§¥π¥μΒΟ![]() Ζ÷Θ§ΦΌ…ηΦΉΕ”÷–ΟΩ»Υ¥πΕ‘ΒΡΗ≈¬ ΨυΈΣ
Ζ÷Θ§ΦΌ…ηΦΉΕ”÷–ΟΩ»Υ¥πΕ‘ΒΡΗ≈¬ ΨυΈΣ![]() Θ§““Ε”÷–
Θ§““Ε”÷–![]() »Υ¥πΕ‘ΒΡΗ≈¬ Ζ÷³eΈΣ
»Υ¥πΕ‘ΒΡΗ≈¬ Ζ÷³eΈΣ![]() Θ§«“Ης»ΥΜΊ¥π’ΐ»Ζ”κΖώœύΜΞ÷°ΦδΟΜ”–”ΑœλΘ§”Ο
Θ§«“Ης»ΥΜΊ¥π’ΐ»Ζ”κΖώœύΜΞ÷°ΦδΟΜ”–”ΑœλΘ§”Ο![]() ±μ Ψ““Ε”ΒΡΉήΒΟΖ÷Θ°
±μ Ψ““Ε”ΒΡΉήΒΟΖ÷Θ°
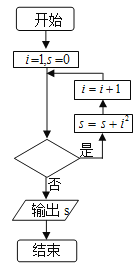
Θ®1Θ©«σ![]() ΒΡΖ÷≤ΦΝ–ΘΜ
ΒΡΖ÷≤ΦΝ–ΘΜ
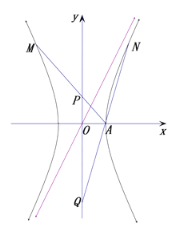
Θ®2Θ©«σΦΉΓΔ““ΝΫΕ”ΉήΒΟΖ÷÷°ΚΆΒ»”Ύ![]() Ζ÷«“ΦΉΕ”Μώ ΛΒΡΗ≈¬ Θ°
Ζ÷«“ΦΉΕ”Μώ ΛΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©Ζ÷≤ΦΝ–ΦϊΫβΈωΘΜΘ®2Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
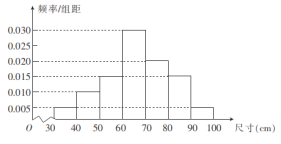
‘ΧβΘ®1Θ©”…Χβ“β÷ΣΘ§![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ
ΒΡΩ…Ρή»Γ÷ΒΈΣ![]() Θ§Ζ÷±π«σ≥ωœύ”ΠΒΡΗ≈¬ Θ§”…¥ΥΡή«σ≥ω
Θ§Ζ÷±π«σ≥ωœύ”ΠΒΡΗ≈¬ Θ§”…¥ΥΡή«σ≥ω![]() ΒΡΖ÷≤ΦΝ–ΘΜΘ®2Θ©”…
ΒΡΖ÷≤ΦΝ–ΘΜΘ®2Θ©”…![]() ±μ ΨΓΑΦΉΕ”ΒΟΖ÷Β»”Ύ
±μ ΨΓΑΦΉΕ”ΒΟΖ÷Β»”Ύ![]() ““Ε”ΒΟΖ÷Β»”Ύ
““Ε”ΒΟΖ÷Β»”Ύ![]() Γ±Θ§
Γ±Θ§![]() ±μ ΨΓΑΦΉΕ”ΒΟΖ÷Β»”Ύ
±μ ΨΓΑΦΉΕ”ΒΟΖ÷Β»”Ύ![]() ““Ε”ΒΟΖ÷Β»”Ύ
““Ε”ΒΟΖ÷Β»”Ύ![]() Γ±Θ§Ω…÷Σ
Γ±Θ§Ω…÷Σ![]() ΓΔ
ΓΔ![]() ΜΞ≥βΘ°άϊ”ΟΜΞ≥β ¬ΦΰΒΡΗ≈¬ ΦΤΥψΙΪ ΫΦ¥Ω…ΒΟ≥ωΦΉΓΔ““ΝΫΕ”ΉήΒΟΖ÷÷°ΚΆΒ»”Ύ
ΜΞ≥βΘ°άϊ”ΟΜΞ≥β ¬ΦΰΒΡΗ≈¬ ΦΤΥψΙΪ ΫΦ¥Ω…ΒΟ≥ωΦΉΓΔ““ΝΫΕ”ΉήΒΟΖ÷÷°ΚΆΒ»”Ύ![]() Ζ÷«“ΦΉΕ”Μώ ΛΒΡΗ≈¬ Θ°
Ζ÷«“ΦΉΕ”Μώ ΛΒΡΗ≈¬ Θ°
‘ΧβΫβΈωΘΚΘ®1Θ©”…Χβ“β÷Σ,![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ
ΒΡΩ…Ρή»Γ÷ΒΈΣ![]() ”…”Ύ““Ε”
”…”Ύ““Ε”![]() »Υ¥πΕ‘ΒΡΗ≈¬ Ζ÷±πΈΣ
»Υ¥πΕ‘ΒΡΗ≈¬ Ζ÷±πΈΣ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ΒΡΖ÷≤ΦΝ–ΈΣ:
ΒΡΖ÷≤ΦΝ–ΈΣ:
|
|
|
|
|
|
|
|
|
|
Θ®2Θ©”…![]() ±μ ΨΓΑΦΉΕ”ΒΟΖ÷Β»”Ύ
±μ ΨΓΑΦΉΕ”ΒΟΖ÷Β»”Ύ![]() ““Ε”ΒΟΖ÷Β»”Ύ
““Ε”ΒΟΖ÷Β»”Ύ![]() Γ±,
Γ±,![]() ±μ ΨΓΑΦΉΕ”ΒΟΖ÷Β»”Ύ
±μ ΨΓΑΦΉΕ”ΒΟΖ÷Β»”Ύ![]() ““Ε”ΒΟΖ÷Β»”Ύ
““Ε”ΒΟΖ÷Β»”Ύ![]() Γ±, Ω…÷Σ
Γ±, Ω…÷Σ![]() ΜΞ≥β, ”÷
ΜΞ≥β, ”÷![]() ,‘ρΦΉΓΔ““ΝΫΕ”ΉήΒΟΖ÷÷°ΚΆΒ»”Ύ
,‘ρΦΉΓΔ““ΝΫΕ”ΉήΒΟΖ÷÷°ΚΆΒ»”Ύ![]() Ζ÷«“ΦΉΕ”Μώ ΛΒΡΗ≈¬ ΈΣ
Ζ÷«“ΦΉΕ”Μώ ΛΒΡΗ≈¬ ΈΣ![]() Θ°
Θ°