Question

【题目】已知函数f（x）＝|x+1|+2|x﹣m|

（1）当m＝2时，求f（x）≤9的解集；

（2）若f（x）≤2的解集不是空集，求实数m的取值范围.

Answer 1

【答案】（1）[﹣2，4]（2）[﹣3，1]

【解析】

（1）当m＝2时，函数f（x）＝|x+1|+2|x﹣2|≤9,对x分类讨论，分别在三个区间，去掉绝对值求解不等式即可求得解集；

（2）若f（x）≤2的解集不是空集，转化为f（x）min≤2成立，又根据|x+1|+|x﹣m|≥|m+1|恒成立，f（x）min＝|m+1|≤2，解得﹣3≤m≤1.

（1）当m＝2时，f（x）＝|x+1|+2|x﹣2|.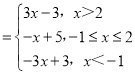

∵f（x）≤9，∴或或，

∴2＜x≤4或﹣1≤x≤2或﹣2≤x＜﹣1，

∴﹣2≤x≤4，

∴不等式的解集为[﹣2，4]；

（2）∵f（x）≤2的解集不是空集，

∴f（x）min≤2.

∵|x+1|+|x﹣m|≥|m+1|，|x﹣m|≥0，

∴f（x）＝|x+1|+2|x﹣m|≥|m+1|，当且仅当x＝m时取等号，

∴|m+1|≤2，∴﹣3≤m≤1，

∴实数m的取值范围为[﹣3，1].