题目内容
【题目】下列四个结论中，错误的序号是___________.①以直角坐标系中
轴的正半轴为极轴的极坐标系中,曲线C的方程为
，若曲线C上总存在两个点到原点的距离为
，则实数
的取值范围是
；②在残差图中，残差点比较均匀地落在水平带状区域中，说明选用的模型比较合适，这样的带状区域宽度越宽，说明模型拟合精度越高；③设随机变量
，若
，则
；④已知
为满足
能被9整除的正数的最小值，则
的展开式中，系数最大的项为第6项.
【答案】234
【解析】
对于①，把极坐标方程化为直角坐标方程，结合圆心与原点的距离关系可求；
对于②，带状区域宽度越宽，说明模型拟合误差越大；
对于③，先利用
求出
，然后再求
；
对于④，先求出
，再利用二项式定理的通项公式求解系数最大的项.
对于①，
化为直角坐标方程为
，半径为
.
因为曲线C上总存在两个点到原点的距离为
，所以
，解得
，故①正确；
对于②，带状区域宽度越宽，说明模型拟合误差越大，故②错误；
对于③，
，解得
；
，故③错误；
对于④，
，
而
，所以
，
所以
的系数最大项为第7项，故④错误；综上可知②③④错误.
练习册系列答案
相关题目
【题目】某地随着经济的发展，居民收入逐年增长该地一建设银行统计连续五年的储蓄存款（年底余额）得到下表：
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
为便于计算，工作人员将上表的数据进行了处理（令
），得到下表：
时间t | 1 | 2 | 3 | 4 | 5 |
储蓄存款z | 0 | 1 | 2 | 3 | 5 |
（1）求z关于t的线性回归方程；
（2）通过（1）中的方程，求出y关于x的回归方程；
（3）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？
附：线性回归方程
，其中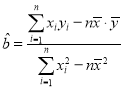
，
.