题目内容
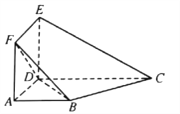
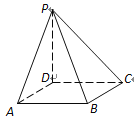
【题目】在四棱锥P–ABCD中，底面ABCD是边长为6的正方形，PD平面ABCD，PD=8．
(1) 求PB与平面ABCD所成角的大小；
(2) 求异面直线PB与DC所成角的大小．
【答案】（1）arctan
（2）arctan
【解析】试题分析：（1）连BD，因为PD平面ABCD，则PBD就是PB与平面ABCD所成的角，解三角形即可求出直线与平面所成的角的正切值；（2）因为AB∥DC，所以PBA就是异面直线PB与DC所成的角，在Rt△PAB中求解即可.
试题解析：
(1)连BD，因为PD平面ABCD，则PBD就是PB与平面ABCD所成的角，
在△PBD中， tan PBD = 
， PBD =arctan
，
PB与平面ABCD所成的角的大小为arctan
；
(2)因为AB∥DC，所以PBA就是异面直线PB与DC所成的角，
因为PD平面ABCD，所以AB⊥PD，又AB⊥AD，所以AB⊥PA，
在Rt△PAB中，PA=10，AB=6，tanPBA=
，PBA=arctan
，
异面直线PB与DC所成角的大小为arctan
．
名校课堂系列答案
【题目】（本小题满分12分）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的宣传费
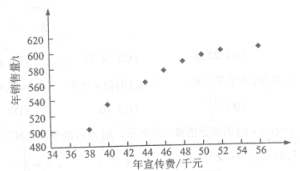
和年销售量
数据作了初步处理，得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中
=
，
=
（Ⅰ）根据散点图判断，
与
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（III）已知这种产品的年利润z与x，y的关系为
，根据（Ⅱ）的结果回答下列问题：
（Ⅰ）当年宣传费
时，年销售量及年利润的预报值时多少？
（Ⅱ）当年宣传费
为何值时，年利润的预报值最大？
附：对于一组数据
,
，……，
,其回归线
的斜率和截距的最小二乘估计分别为：
，
【题目】前几年随着网购的普及，线下零售遭遇挑战，但随着新零售模式的不断出现，零售行业近几年呈现增长趋势，下表为
年中国百货零售业销售额（单位：亿元，数据经过处理， 
分别对应
）：
年份代码 | 1 | 2 | 3 | 4 |
销售额 | 95 | 165 | 230 | 310 |
（1）由上表数据可知，可用线性回归模型拟合
与
的关系，请用相关系数加以说明；
（2）建立
关于
的回归方程，并预测2018年我国百货零售业销售额；
（3）从
年这4年的百货零售业销售额及2018年预测销售额这5个数据中任取2个数据，求这2个数据之差的绝对值大于200亿元的概率.
参考数据：
， 
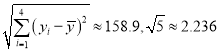
参考公式：相关系数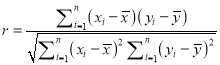
，回归方程
中斜率和截距的最小二乘估计公式分别为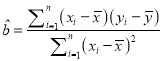
， 
.
