题目内容
若圆x2＋y2＝4与圆x2＋y2＋2ax－6＝0(a＞0)的公共弦的长为2
，则a＝________.
1
【解析】x2＋y2＋2ax－6＝0(a>0)可知圆心为(－a,0)，半径为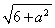
，两圆公共弦所在方程为(x2＋y2＋2ax－6)－(x2＋y2)＝－4，即x＝
，所以有
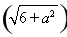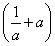2－
2＝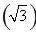
2解得a＝1或－1(舍去)．
练习册系列答案
相关题目
题目内容
若圆x2＋y2＝4与圆x2＋y2＋2ax－6＝0(a＞0)的公共弦的长为2，则a＝________.
1
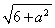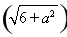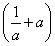【解析】x2＋y2＋2ax－6＝0(a>0)可知圆心为(－a,0)，半径为，两圆公共弦所在方程为(x2＋y2＋2ax－6)－(x2＋y2)＝－4，即x＝，所以有2－2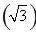＝2解得a＝1或－1(舍去)．
