题目内容

【题目】若圆上有四个不同的点到直线的距离为2，则的取值范围是(　　)

A. (－12，8) B. (－8，12) C. (－13，17) D. (－17，13)

【答案】C

【解析】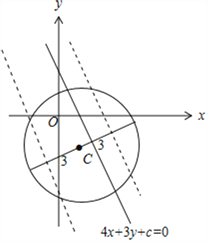圆C：x2+y2﹣2x+4y﹣20=0化为（x﹣1）2+（y+2）2=25，

则圆心C为（1，﹣2），半径r=5．

若圆C：（x﹣1）2+（y+2）2=25有四个不同的点到直线l：4x+3y+c=0的距离为2，

则圆心C（1，﹣2）到直线l的距离d＜3，

即解得：﹣13＜c＜17，∴c的取值范围是（﹣13，17）．

故选：C．

点睛: 由题意画出图形，若圆C：（x﹣1）2+（y+2）2=25有四个不同的点到直线l：4x+3y+c=0的距离为2，则圆心C（1，﹣2）到直线l的距离d＜3，由此列关于c的不等式得答案．

练习册系列答案
相关题目

【题目】

有甲、乙、丙、丁四名网球运动员，通过对过去战绩的统计，在一场比赛中，甲对乙、丙、丁取胜的概率分别为.

（Ⅰ）若甲和乙之间进行三场比赛，求甲恰好胜两场的概率；

（Ⅱ）若四名运动员每两人之间进行一场比赛，设甲获胜场次为，求随机变量的分布列及期望．

【题目】已知函数f（x）=x2+（a+8）x+a2+a﹣12（a＜0），且f（a2﹣4）=f（2a﹣8），则 的最小值为（ ）
A.
B.
C.
D.

【题目】已知椭圆（）的离心率为， 分别是它的左、右焦点，且存在直线，使关于的对称点恰好是圆（）的一条直线的两个端点.

（1）求椭圆的方程；

（2）设直线与抛物线（）相交于两点，射线， 与椭圆分别相交于点，试探究：是否存在数集，当且仅当时，总存在，使点在以线段为直径的圆内？若存在，求出数集；若不存在，请说明理由.

【题目】已知过原点的动直线与圆相交于不同的两点．

（1）求线段的中点的轨迹的方程；

（2）是否存在实数，使得直线与曲线只有一个交点？若存在，求出的取值范围；若不存在，请说明理由．

【题目】如图,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.

(1)当θ=时,求点A的位置,使矩形ABOC的面积最大,并求出这个最大面积;

(2)当θ=时,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积.

【题目】某保险公司有一款保险产品的历史收益率（收益率=利润÷保费收入）的频率分布直方图如图所示：

（Ⅰ）试估计平均收益率；

（Ⅱ）根据经验，若每份保单的保费在20元的基础上每增加元，对应的销量（万份）与（元）有较强线性相关关系，从历史销售记录中抽样得到如下5组与的对应数据：

据此计算出的回归方程为.

（i）求参数的估计值；

（ii）若把回归方程当作与的线性关系，用（Ⅰ）中求出的平均收益率估计此产品的收益率，每份保单的保费定为多少元时此产品可获得最大收益，并求出该最大收益.

【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度，选了某小区的100位居民调查结果统计如下:

（1）根据已有数据，把表格数据填写完整；

（2）能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关？

（3）已知在被调查的年龄大于50岁的支持者中有5名女性，其中2位是女教师,现从这5名女性中随机抽取3人，求至多有1位教师的概率.

附: ， .

【题目】数列{an}中，a1＝，前n项和Sn满足Sn＋1－Sn＝()n＋1(n∈N*)．

(1)求数列{an}的通项公式an以及前n项和Sn；

(2)若S1，t(S1＋S2)，3(S2＋S3)成等差数列，求实数t的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网